Contest Info

date: 2019.03.16 13:40-18:40

practice link

Solutions

A. Amalgamated Artichokes

签到题。

B. Asteroids

题目大意：两个凸多边形在做匀速直线运动，问它们什么时刻相交的面积最大。

题解：如果一段时间这两个多边形的任意两条边的相交关系不变，那么相交面积就是一个关于时间的二次函数。在区间内三分即可。

C. Catering

题目大意：通过枚举题意，我们得到这样的题面：给出数列\(1,\cdots,n\)分成不超过\(k\)个子序列（\(1\le n,k\le100\)），数字\(i\)作为子序列开头的代价是\(a_{0,i}\)，跟在数字\(j<i\)后面的代价是\(a_{j,i}\)，求最小的代价。

题解：建图跑有流量下界的费用流：

• 从\(S\)到\(0\)号点连流量为\([0,k]\)，费用为\(0\)的弧；
• 将\(1,\cdots,n\)每个点拆为\(u(i)\)和\(v(i)\)两个点，并从\(u(i)\)向\(v(i)\)连流量为\([1,1]\)，费用为\(0\)的弧；
• 从\(0​\)向每个\(u(i)​\)连流量为\([0,1]​\)，费用为\(a_{0, i}​\)的弧；
• 从每个\(v(i)​\)向\(T​\)连流量为\([0,1]​\)，费用为\(0​\)的弧；
• 从每个\(v(i)\)向\(u(j)\)（\(i<j\)），连流量为\([0,1]\)，费用为\(a_{i,j}\)的弧；

从\(S\)到\(T\)的最小费用可行流就是答案。

D. Cutting Cheese

题目大意：给你一个正方体，里面有若干个球形的洞，要求在平行于 \(xOy\) 平面的地方把它切成 \(s\) 块，使得每块体积相等。

题解：简单积分。

H. Qanat

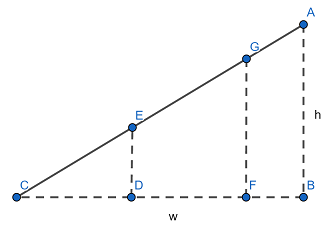
题目大意：题面好难读啊。。如图，大意是有一个 \(w\times h(w>h)\) 的梯田，现在要在地下挖一些沟渠来灌溉。其中 \(AB\) 和 \(BC\) 的位置是固定必须挖的，另外还要再挖 \(n\) 条沟渠，这些沟渠只要是竖直方向即可（例如 \(DE,FG\)），横坐标可以是 \([0,w]\) 中的任意实数。挖出来的土必须要送到 \(AC\)（地面）上，每个位置的土可以沿沟渠任意的水平方向及竖直方向走，代价即为最短距离，总代价为 \(\int d(x)\)。要求你合理安排这 \(n\) 条沟渠的位置，使得总代价最小。

题解：设 \(f_{i}(x)\) 表示再挖 \(i\) 条沟渠，\(w\) 和 \(h\) 等比例放缩成 \(w=x\)（即 \(h:=\frac{hx}{w}\)）时最小的代价。显然有 \(\displaystyle{f_{0}(x)=(\frac{1+\frac{h}{w}}{2})^{2}x^{2}}\)。考虑由 \(f_{i}(x)\) 转移到 \(f_{i+1}(x)\)，我们有 \[ \begin{aligned} f_{i+1}(x)=\min_{0\le x'\le x}\left(f_{i}(x')+2\left(\frac{\frac{h}{w}(x+x')+x-x'}{2}\right)^{2}-\left(\frac{h}{w}x'\right)^{2}\right) \end{aligned} \] 显然也是个关于 \(x\) 和 \(x'\) 的二次型，可以得到 \(x'=kx\)（\(k\) 由二次型的系数确定）时取最小值，\(f_{i+1}(x)\) 仍与 \(x^{2}\) 成正比。当然最小值落在 \([0,x]\) 中间需要证明，这里就不赘述了。

另外积分的结果是要除 \(2\) 的，上面为了方便没有写，不过不影响做法。

I. Ship Traffic

题目大意：在一个游泳池分为东西方向的\(n\le1e5\)条赛道，每条赛道宽\(w\)。有一个质点在时间\([t_1,t_2]\)的某个时间从原点出发，以匀速\(u\)向北穿越这个游泳池。第\(i\)条赛道中有\(m_i\)个人，沿方向\(East\)或者\(West\)以速度\(v\)匀速移动，初始时他们的头部相对于过原点南北方向的这条直线的距离是\(p_{i,j}\)，长度为\(l_{i,j}\)。要求质点从到达第\(i\)条赛道到离开为止，不可以有人穿过这条南北方向的分界线。求最大的可行的开始时间区间长度。

题解：直接对于每个人计算出它让哪一个区间的开始时间不行了，然后做一下线段覆盖，时间复杂度\(O(n\log{n})\)。

J. Tile Cutting

题目大意：设 \(f(x)\) 为面积为 \(x\) 的不同形状，不与坐标轴平行的格点平行四边形的数量，求 \(f(l),\cdots,f(r)\) 中的最大值。

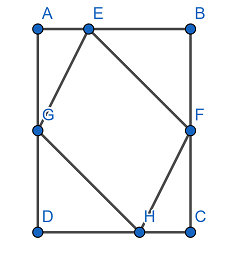
题解：如图，设 \(BE=x_{1},BF=y_{1},FC=y_{2},CH=x_{2}\)，显然 \(x_{1},x_{2},y_{1},y_{2}\) 与一个平行四边形一一对应，而该四边形的面积恰为 \(x_{1}y_{1}+x_{2}y_{2}\)。我们设 \(\Sigma(x)=\sum_{i=1}^{+\infty}\sigma(x)\)，那么 \([x^{i}]\Sigma^{2}(x)\) 即为面积为 \(i\) 的多边形数量，FFT 加速即可。

L. Weather Report

题目大意：有 \(4\) 种天气，在 \(n\) 天内每天会随机出现一种，每天每种天气概率相等，且每天相互独立。求 \(4^{n}\) 种可能的天气的哈夫曼编码。

题解：注意到至多只有 \(\mathcal{O}(n^{4})\) 种不同的状态。用 map 维护，时间复杂度 \(\mathcal{O}(n^{4}\log n)\)。