Contest Info

date 2017.08.19 12:00-17:00

practice link

Solutions

A. Vertex Cover

题目大意：给你一个求最小点覆盖的贪心算法：每次选择度数最大的点（如果度数相同，选择标号最大的点），然后将其加入答案集合，删掉相关的边。不断操作直到没有边。让你构造一个图，使得该算法求出的解至少是你给出的一个解的三倍。

题解：

如图所示，我们构造一个二分图 \(G=(L+R,E)\)。设 \(\mid L\mid =n\)，我们将 \(R\) 中的点分为 \(n\) 类，分别为 \(R_1,\dots, R_n\)。其中 \(\mid R_i\mid = \lfloor\frac{n}{i}\rfloor\)，并且 \(R_i\) 中的每个点向 \(L\) 部的 \(i\) 个点连边，同一类点连的 \(L\) 部的点互不相同。 \(L\) 部中度数最大的点（第 \(1\) 个点）的度数为 \(R\) 部中点的种类数，而 \(R\) 部中类别 \(i\) 的点度数为 \(i\)。显然题目所给的算法，会从右向左依次选择 \(R\) 部中的点作为一个点覆盖。而只选择 \(L\) 部的点也是一个点覆盖。

此时，我们得到的解的倍数为 \(\mid R\mid /\mid L\mid\)，其中 \(\mid L\mid =n\)，且 \(\mid R\mid = \sum\limits_{i=1}^n \lfloor \frac{n}{i}\rfloor\)。稍微计算一下发现我们取 \(n=15\) 就可以满足要求了。

B. Party

题目大意：给出一个\(A\) 到 \(B\) 的二分图，\(A\) 中每个点权值为 \(a_i\)，\(B\) 中每个点权值为 \(b_i\)。有 \(q\) 次询问，每次询问给出一个正整数 \(g\)，问只考虑标号是 \(g\) 的倍数的子图，有多少非空的顶点的子集 \(V\) ，使得存在一个匹配盖住 \(V\)（可以多覆盖不在 \(V\) 中的点）。\(|A|,|B|\le20,q\le10\)。

题解：由广义 Hall 引理，如果存在一个匹配 \(\text{Match}(X)\) 能覆盖点集 \(X\subseteq A\)，并且也存在一个匹配 \(\text{Match}(Y)\) 能覆盖点集 \(Y\subseteq B\)，那么一定存在一个匹配 \(\text{Match}(X+Y)\) 能覆盖 \(X+Y\)。于是，问题可以转化为对于每一组询问，分别计算原图对应的子图中两部分顶点集的合法（存在匹配能够覆盖）的子集数量。

又根据 Hall 婚配定理，二分图 \(G=(A'+B',E)\) 存在一种匹配 \(\text{Match}(X)\) 能覆盖点集 \(X\subseteq A'\) 的充要条件为：对 \(\forall X'\)，如果 \(X'\subseteq X\)，那么 \(|X'|\le\sum\limits_{y\in B'}[\exists x(x\in X'\land (x\to y)\in E])\)（任意大小为 \(k\) 的子集连接至少 \(k\) 个点）。

于是，我们可以枚举 \(A'\) 的子集 \(set\)，递推的计算出\(\sum\limits_{y\in B'}[\exists x(x\in set\land (x\to y)\in E)]\)。令 \(go[set]\) 表示与 \(set\) 相连的 \(B'\) 中的点集。先预处理出与每个点相连的 \(B'\) 中的点集，之后递推的转移方程为 \(go[set]=go[set\setminus \text{lowbit}(set)]\cup go[\text{lowbit}(set)]\)。然后我们枚举集合 \(set\) 验证其是否合法，因为不合法的状态有传递性，所以只需要验证它的大小为 \(\mid set\mid -1\) 的子集即可。另一边的情况类似。时间复杂度为 \(\mathcal{O}(q(n2^n+m2^m))\)，空间复杂度为 \(\mathcal{O}(2^n+2^m)\)。

C. Friend-Graph

题目大意：给你一个简单无向图，让你判断是否存在三元环，或者反图是否存在三元环。

题解：由 Ramsey’s theorem 我们知道 \(R(3,3)=6\)，所以当 \(n\geq 6\) 的时候一定存在。只需要暴力判断 \(n<6\) 的情况即可。

D. A Secret

题目大意：给定两个字符串 \(S_1,S_2\)，令 \(\text{Suffix}(S_2,i)=S_2[i\dots len]\)。设 \(L_i,N_i\) 分别表示 \(\text{Suffix}(S_2,i)\) 的长度以及它在串 \(S_1\) 中的出现次数。求 \(\sum\limits_{i=1}^{len} L_iN_i\)。

题解：直接将两个串反过来，然后对串 \(S_1\) 建立后缀自动机，跑串 \(S_2\) 可以很简单实现。但是因为 \(\mid \Sigma \mid=52\)，所以清空后缀自动机的常数很大，会超时。我们考虑用 kmp 来做。

我们对 \(S_2\) 建立 kmp 的 fail 数组，并且对于每个前缀，我们都记录一个 \(\text{cnt}\) 表示 fail 链上所有的前缀长度之和。那么我们去跑串 \(S_1\) 的时候，每匹配到一个位置，这个位置对应的 fail 链上的前缀都出现一次，贡献为 \(\text{cnt}\)。

或者我们记录每个位置匹配成功地次数，然后沿着 fail 链累加上去，最后再枚举每个前缀计算答案。

E. CaoHaha’s staff

签到题，找规律打表即可。

F. Subsequence Count

题目大意：给定一个长度为 \(n\) 的 \(0/1\) 串，和 \(q\) 次操作，操作分为两种：

• 翻转 \([l,r]\) 中的每一位
• 计算 \([l,r]\) 中本质不同的子序列个数

题解：我们先考虑怎么计算 \([1,n]\) 的本质不同的子序列个数。我们令 \(dp[i][0/1]\) 表示到第 \(i\) 位为止，以 \(0/1\) 结尾的本质不同的子序列的个数。如果第 \(i\) 位是 \(0/1\)，那么显然有：

\[ \begin{aligned} dp[i][0/1] &= dp[i-1][0] + dp[i-1][1] + 1\\ dp[i][1/0] &= dp[i-1][1/0] \end{aligned} \]

其中 \(dp[0][0]=dp[0][1]=0\)。容易发现第 \(i\) 位从 \(i-1\) 位而来的转移方程，只与第 \(i\) 位是 \(0\) 还是 \(1\)有关，我们用矩阵乘法来表示这个状态转移：

\[ \left( \begin{array}{ccc} dp_{i-1,0} & dp_{i-1,1} & 1 \end{array} \right) \cdot \mathbf{M_{0/1}}= \left( \begin{array}{ccc} dp_{i,0} & dp_{i,1} & 1 \end{array} \right) \]

其中 \(\mathbf{M_0},\mathbf{M_1}\) 分别表示第 \(i\) 位是 \(0/1\) 的转移矩阵。

\[ \mathbf{M_0} = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right), \mathbf{M_1} = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right) \]

那么我们每次询问区间 \([l,r]\) 的时候，只需要知道 \(\mathbf{A}=\prod_{i=l}^r \mathbf{M_{s[i]}}\)，那么有：

\[ \left( \begin{array}{ccc} 0 & 0 & 1 \end{array} \right) \cdot \mathbf{A}= \left( \begin{array}{ccc} dp_{r,0} & dp_{r,1} & 1 \end{array} \right) \]

我们用一个线段树来维护这个乘积即可。对于修改操作，我们只需要将对应的矩阵的前两列交换，再将前两行交换即可。

G. Palindrome Function

签到题，数位 dp 。

H. The Karting

题目大意：给出一个分为 \(n-1\) 段的直线段赛道，左端点为 \(1\)，右端点为 \(n\)。第 \(i\) 段赛道（连接点 \(i\) 和 \(i+1\) 的直线段）的难度为 \(d_i\)，选手做一次 \(180^\circ\) 的转弯的难度为 \(d_0\)。现在要选出恰好 \(m\) 个点，并把这 \(m\) 个点划分为若干个不相交且大小不小于 \(2\) 的集合。每个集合对应一次比赛，它的难度为从集合的其中一个点出发，依次遍历其它所有点，最后回到起点（回到起点也要做出一次 \(180^\circ\) 转弯），所经过的道路的难度，与 \(180^\circ\) 转弯的难度之和。给出 \(m\)，求最大难度和。\(1\le n,m,|d_i|\le100\)。

题解：将一次比赛的路径画出来可以发现是若干条线段，覆盖任意一段赛道的线段数量为偶数，而且只有经过做 \(180^\circ\) 转弯的点会使得覆盖的线段数量发生变化，且只会变化 \(2\)。令 \(f[i][j][k]\) 表示前 \(i\) 个点选出恰好 \(j\) 个点，覆盖第 \(i\) 段赛道的直线段为 \(2k\) 的最大难度和。则 \(f[i][j][k]\) 有四种转移：

• 不选第 \(i\) 个点，难度为\(f[i-1][j][k]+d_{i-1}\times2k\)
• 选第 \(i\) 个点，但是不在第 \(i\) 个点处转向（需要 \(j>0\)），难度为 \(f[i-1][j-1][k]+d_{i-1}\times2k\)
• 选第 \(i\) 个点，并且在第 \(i\) 个点处转向朝向点 \(n\) 方向（需要 \(j>0\land k>0\)），难度为 \(f[i-1][j-1][k-1]+d_{i-1}\times2(k-1)+d_0\)
• 选第 \(i\) 个点，并且在第 \(i\) 个点处转向朝向点 \(1\) 方向（需要 \(j>0\land k<n\)），难度为 \(f[i-1][j-1][k+1]+d_{i-1}\times2(k+1)+d_0\)

初始状态为 \(f[1][0][0]=0,f[1][1][1]=d_0\)，答案为 \(f[n][m][0]\)。时空复杂度都是 \(\mathcal{O}(n^2m)\)。

I. The Designer

题目大意：给你两个内切的圆，然后在它们相切的缝隙中依次添加一些小圆和已有的圆相切（具体见题图），求添加 \(n\) 个小圆的总面积。

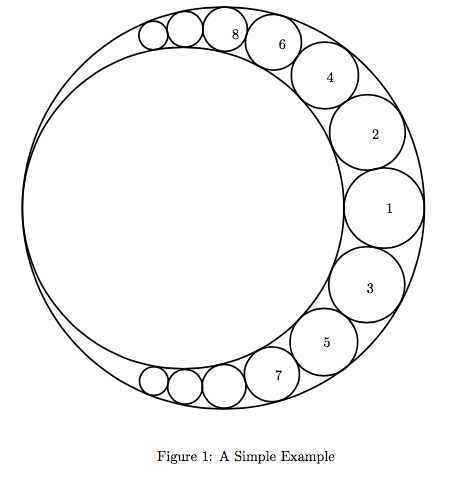
题解：为讨论方便，只考虑一侧的小圆。设较大的圆半径为 \(R\) ，较小的圆半径为 \(r\) ，第 \(i\) 个小圆半径为 \(r_{i}\) 。根据 Descartes’ theorem，和这三个圆都相切的圆的半径 \(x\) 满足：

\[ (\frac{1}{r}+\frac{1}{x}+\frac{1}{r_{i}}-\frac{1}{R})^{2}=2(\frac{1}{r^2}+\frac{1}{x^2}+\frac{1}{r_{i}^2}+\frac{1}{R^2}) \]

我们就得到了一个二次方程，它的两个根恰好是 \(r_{i-1}\) 和 \(r_{i+1}\) ，所以根据韦达定理有 \(\displaystyle \frac{1}{r_{i+1}}=\frac{2}{r}+\frac{2}{r_{i}}-\frac{2}{R}-\frac{1}{r_{i-1}}\) 。由于 \(T\cdot n\) 太大，直接计算完 \(n\) 会超时，所以当小圆很小时（具体来说，应该比精度限制还要小，因为如果在当前圆停止计算，精度误差应该是剩下的所有小圆的面积和），要停止计算。

coldwater’s comment

还可以将两个大圆关于两圆切点反演为两条平行直线，然后剩余的小圆则全部反演为夹在两直线间的一堆相切的小圆。也可以推出上式。

J. Graph Of Zhuper

题目大意：求 \(\displaystyle \sum\limits_{G为n阶有标号简单无向图}Zhu(G)\) 。其中 \(Zhu(G)=\gcd(size_{1},\cdots,size_{k})\) ， \(size_{1},\cdots,size_{k}\) 表示 \(G\) 的 \(k\) 个连通块的大小。

题解： 法一： 先计算连通图的数量。设 \(f(n)\) 表示 \(n\) 阶有标号连通简单无向图的个数。则有（减去枚举编号为 \(1\) 的点所在连通块的大小 \(i\)）：

\[ \begin{aligned}\\ f(n)&=2^{n\choose 2}-\sum_{i=1}^{n-1}{{n-1}\choose {i-1}}\cdot f(i)\cdot2^{{n-i}\choose 2}\\ &=2^{n\choose 2}-(n-1)!\sum_{i=1}^{n-1}\frac{f(i)}{(i-1)!}\cdot\frac{2^{{n-i}\choose 2}}{(n-i)!} \end{aligned}\\ \]

可以用分治乘法加 FFT 来计算。

设 \(g_d(n)\) 表示所有连通块大小都能被 \(d\) 整除的 \(nd\) 阶有标号简单无向图的方案数，则所求为：

\[ \begin{aligned}\\ \text{ans}&=\sum_{i=1}^ni \sum_{G}[Zhu(G)=i]\\ &=\sum_{i=1}^{n}i\sum_{i|d}\mu(\frac{d}{i})g_{d}(\frac{n}{d})\\ &=\sum_{d=1}^{n}g_{d}(\frac{n}{d})\sum_{i|d}\mu(\frac{d}{i})i\\ &=\sum_{d=1}^{n}\varphi(d)g_{d}(\frac{n}{d})\\ &=\sum_{d|n}\varphi(d)g_{d}(\frac{n}{d}),(g_d(\frac{n}{d})=0 \text{ iff } d\nmid n)\\ \end{aligned}\\ \]

对每个 \(n\) 的约数 \(d\) ，我们考虑 \(g_{d}(n)\) 如何计算，有（加上枚举编号为 \(1\) 的点所在连通块是 \(d\) 的倍数 \(i\)）：

\[ \begin{aligned}\\ g_{d}(n)&=f(nd)+\sum_{i=1}^{n-1}{{nd-1}\choose {id-1}}f(id)g_{d}(n-i)\\ &=f(nd)+(nd-1)!\sum_{i=1}^{n-1}\frac{f(id)}{(id-1)!}\cdot\frac{g_{d}(n-i)}{(nd-id)!}\\ \end{aligned}\\ \]

仍然可以分治乘法加 FFT 解决，复杂度 \(\mathcal{O}(\sigma_{1}(n)\log^{2}n)\) 。

法二：（icpc-camp 题解做法）：求 \(g_{d}(n)\) 可以使用生成函数来解决。

\[ \begin{aligned}\\ g_{d}(n)&=\sum_{i=1}^{n}\frac{1}{i!}\sum_{k_{1}+\cdots+k_{i}=n}\frac{(nd)!}{(k_{1}d)!\cdots(k_{i}d)!} f(k_{1}d) \cdots f(k_{i}d)\\ &=(nd)!\sum_{i=1}^{n}\frac{1}{i!}\sum_{k_{1}+\cdots+k_{i}=n}\frac{f(k_{1}d)}{(k_{1}d)!} \cdots \frac{f(k_{i}d)}{(k_{i}d)!} \end{aligned}\\ \]

我们令 \(\displaystyle h(x)=\sum_{i=1}^{n}\frac{f(id)}{(id)!}x^{i}\) ，则答案就是 \(\displaystyle \sum_{i=1}^{n}\frac{h^{i}(x)}{i!}\) 的第 \(n\) 项系数乘以 \((nd)!\) 。注意到 \(i=0\) 和 \(i>n\) 的 \(\displaystyle \frac{h^{i}(x)}{i!}\) 对答案没有影响，所以我们可以转化为计算 \(\displaystyle \sum_{i=0}^{\infty}\frac{h^{i}(x)}{i!}=e^{h(x)}\) 。

这样这部分的复杂度就变成了 \(\mathcal{O}(\sigma_{1}(n)\log n)\) ，但是由于多项式 exp 巨大的常数，实测和我的解法时间似乎差不多，稍微快一点点。

K. Convolution Layer

题目大意：给你两个四维矩阵 \(I\in {\{-1, 1\}}^{n\times c\times h_i\times w_i}\) 和 \(W\in {\{-1, 1\}}^{m\times c\times h_w\times w_w}\)。让你求 \(O\in \mathbb{R}^{n\times m\times h_o\times w_o}\)，其中 \(h_o=h_i-h_w+1,w_o=w_i-w_w+1\)，并且有：

\[ O[i][j][x][y]=\sum_{k=0}^{c-1}\sum_{i'=0}^{h_w-1}\sum_{j'=0}^{w_w-1}I[i][k][x+i'][y+j']\cdot W[j][k][i'][j'] \]

要求输出：

\[ \sum_{i=0}^{n-1}\sum_{j=0}^{m-1}\sum_{x=0}^{h_o-1}\sum_{y=0}^{w_o-1}O[i][j][x][y]\cdot f(i, j, x, y) \]

其中 \(f(i, j, x, y)\) 是一个关于 \(i, j, x, y\) 的函数。

题解：我们交换枚举的顺序，先枚举 \(i, j, k\)，那么要求的就是一个经典的问题：在一个大矩阵（\(I[i][k]\)）中，对于小矩阵（\(W[j][k]\)）能放的每个位置（\(x, y\)），求一个对应位置的乘积的和，再乘上一个关于 \(i,j,x,y\) 的函数。因为矩阵元素只有 \(-1,1\)，并且观察到负负得正的性质和异或相同，所以我们分别用 \(1/0\) 来替代 \(-1/1\)。然后对大矩阵的每一行压位，对小矩阵整个串起来压位。小矩阵的大小是 \(11\times 11=121\) 的，所以可以用 __int128 压位。

接下来枚举列 \(y\)，然后逆序枚举 \(x\)，将以 \((x,y)\) 为左上角的子矩形从 \(I[i][k]\) 中抠出来，然后与 \(W[j][k]\) 异或。\(x\) 变化的时候只需要删除一行，再添加一行。复杂度为 \(\mathcal{O}(n\cdot m\cdot c\cdot h_ow_o\cdot h_ww_w/32)\)。对 \(I[i][k]\) 的行压位时，因为只有 \(56\) 位，所以用 long long 会快一些。

Replay and Summary

Replay

D 上来看了看 C 题和 D 题，然后让 W 来做 D 这个字符串。D 说直接后缀自动机建好跑一次就可以了，然后 W 写了之后直接 re。仔细看题发现有大写字母，开始改，然后隐约觉得不对劲但还是交了，然后就 tle 了，因为 52 的数组常数太大。W 决定从头好好想想，然后 D 去想 C 题。

过了一会儿 W 觉得直接 kmp 就能写了，就开始写，写完之后就 a 掉了。D 在想 C 题的时候，W 说了一句这不是离散书上的那题吗，当 n >= 6 的时候无解。然后 D 没听明白，W 也否认了自己的看法。导致 D 去讨论各种情况还 mle 了一次。改了改也过掉了。

Z 默默看题一直到这个时候，然后觉得 E 题打个表就行了结果打表打少了又 wa 了一次。然后 Z 开始写 G 题这道数位 dp。写完也过掉了。

过掉四题的弊队开始爆炸。这时开了 A F I 三题。A 题简单画了画图不太会，F 题是真的不会， I 题 Z 本来想预处理，但是发现空间很小，然后就想二分，又觉得会超时。就一直僵硬到了最后一个小时。

W 先是觉得 A 题 m=0 就行了，结果题目很不讲道理地又没说 m 不等于 0，又不让过。W 又想起了之前被否认的二分图，看了看 A 题题目给出的 wiki，然后构造了一发就过了。接下来的时间 W 和 D 在 F 和 H 之间徘徊，还是做不出来，而 Z 在不断地提交 I 题，一直 wa 和 tle。

coldwater

感觉没什么好说的，就是太多东西不会了，太多定理不知道，还是得学习一个。

ShinriiTin

一开始罚时 +3，然后心态有点崩。C 忘记了自己以前证明过的结论，写的有点复杂了，浪费了时间，还 mle 一发。D 我又思维僵化带偏了让 W 去写 SAM，之后因为多组数据要清数组，字符集太大导致清数组时间耗费太大就 tle 了。冷静想了一下，其实就是一个 Kmp 的事情。然后 A 半天构造不出来，就完全爆炸了。F 和 H 的 dp 明明都很简单，但是场上完全没有向这个方向考虑。 之后和 Z 说了一下 J 可以反演之后枚举 n 约数什么的，然后连通图个数可以分治乘法什么的，但是 Z 忙着搞 I，我也很久没做复杂的数学题，不太敢自己推，就摸了。之后要想办法找时间加强一下数学和几何，可以稍微分担一下 Z 的工作。

zhongzihao

太菜了，菜到没话说，还是滚去补题和刷题吧。

update:其实 J 还是会做的，当时不应该去写计算几何，虽然这么说有点马后炮就是了。