Contest Info

date 2017.08.01 12:00-17:00

practice link

Solutions

A. simple counting problem

题目大意：给你 \(m, n, b, c\) ，求满足 \(0\le x_{i} \le b^{i} - c\) 且 \(\sum_{i=1}^{m} x_i< n\) 的数列 \(\{x_i \}\) 有多少个。

题解：给数列补上一个 \(x_{m+1}=n-\sum_{i=1}^{m}x_{i}\) ，答案即为求 \(x_{1}+\cdots+x_{m+1}=n+m\) 的正整数解的个数。如果没有上界限制，这就是一道水题，而在题目的限制下，我们考虑容斥解决。 显然 \(\displaystyle ans = \sum_{S\subseteq [1,n]}(-1)^{|S|} { {n+m-1-\displaystyle \sum_{i\in S}(b^{i}-c+1)} \choose {m}}\) ，直接计算的复杂度有 \(2^{50}\) ，显然不能满足题目要求。我们注意到，如果把组合数写成 \(\sum_{i\in S}b^{i}\) 的 \(m\) 次多项式，则这个多项式的系数只和 \(|S|\) 有关，我们尝试在这方面加速。设 \(dp[i][j][k]\) 表示 \(\displaystyle \sum_{S\subseteq[1,i], |S|=j}(\sum_{i\in S}b^{i})^{k}\) ，容易写出转移方程：

\[ dp[i][j][k]= \left\{ \begin{aligned} &0,&i<j\\ &1,&j=k=0\\ &dp[i-1][j][k]+b^{ik},&j=1\\ &dp[i-1][j][k]+\sum_{u=0}^{k}{k \choose u}b^{iu}dp[i-1][j-1][k-u],&others \end{aligned} \right. \]

固定 \(|S|\) , 可以发现，组合数不为 \(0\) 的条件是 \(\sum_{i\in S}b^{i} < n+|S|(c-1)\) ，我们把 \(n+|S|(c-1)\) 写成一个 \(b\) 进制数，然后就可以数位 \(dp\) 枚举子集，利用刚刚预处理的东西配合二项式定理就很容易做了（这个实在没法写式子，偷个懒）。复杂度 \(O(m^{4})\) 。

听说是个原题 梦中的题面

B. Kanade’s convolution

题目大意：给你两个数列 \(A[0, \dots, 2^{m}-1]\) 和 \(B[0, \dots ,2^{m}-1]\) ，定义 \(\displaystyle C[k]=\sum_{i\land j=k}A[i \oplus j]* B[i\lor j]\) ，求 \(\sum_{i=0}^{2^{m}-1}C[i]*1526^{i}\) 。

题解：

法一：统计每个 \(A[i]*B[j]\) 给答案做了多少贡献。 观察容易发现，只有当 \(i\land j=i\) 时， \(A[i]*B[j]\) 才给答案做贡献。得到 \(A[i]*B[j]\) 的情况有 \(2^{bitcnt(i\land j)}=2^{i}\) 种，它给 \(C[i\oplus j]\) 贡献答案，也就是说还要乘上 \(1526^{i\oplus j}\) ，即答案为 \(\sum_{i=0}^{2^{m}-1}2^{bitcnt(i)}*A[i]*\displaystyle \sum_{i\land j=i}1526^{i\oplus j}B[j]\) 。

现在的问题就变成了对于每个 \(i\) 计算 \(\displaystyle \sum_{i\land j=i}1526^{i\oplus j}B[j]\) ，这可以用一个 \(m\) 维后缀和来计算。设 \(dp[i][j]\) 表示后 \(j\) 位大于等于 \(i\) 的后 \(j\) 位（从最低位为\(1\) 开始编号） ， 剩余的位等于 \(i\) 的对应位，这样的数的答案的后缀和。 \(dp\) 方程为： \[ \left\{ \begin{aligned} &dp[i][j]=B[i],&j=0\\ &dp[i][j]=dp[i\lor 2^{j-1}][j-1]*1526^{2^{j-1}}+dp[i][j-1],&i\land 2^{j-1}=0 \end{aligned}\\ \right. \]

对于 \(i\) 所要求的答案即为 \(dp[i][m]\) 。复杂度 \(O(2^{m}\cdot m)\) 。

法二：由上面的讨论容易知道：

\[ \begin{aligned}\\ C[k]&=\sum_{i\oplus j=k}[i\land j=i] *a[i]*b[j]*2^{bitcnt(i)}\\ &=\sum_{i\oplus j=k}[bitcnt(j)-bitcnt(i)=bitcnt(k)]*a[i]*b[j]*2^{bitcnt(i)} \end{aligned}\\ \]

就可以用元素为多项式的 \(FWT\) 来加速了，复杂度 \(O(2^{m}\cdot m^{2})\) ，有些卡常，实现时要非常小心。

C. Kanade’s sum

题目大意：给出一个 \(1\) 到 \(n\)（\(n \leq 5 \times 10^5\)） 的排列，和一个正整数 \(K\)（\(K \leq \min(n,80)\)），求所有长度不小于 \(K\) 的区间的第 \(K\) 大的数之和。

题解：先枚举作为第 \(K\) 大的数字 \(x\) ，设 \(x\) 在排列中的位置为 \(i\)，再枚举一个非负整数 \(k\)。如果我们能求得有多少个不同的 \(l\) 满足区间 \([l,i]\) 中大于 \(x\) 的数的个数等于 \(k\)，设这样的 \(l\) 有 \(L\) 个。同时求得有多少个（\(R\) 个）不同的 \(r\) 满足区间 \([i,r]\) 中大于 \(x\) 的数的个数等于 \(K-k-1\)，则以 \(x\) 作为第 \(K\) 大的区间一共有 \(L \times R\) 个。接下来，我们要考虑如何高效率地去求这些信息。

我们从小到大枚举 \(x\)，当计算完当前的 \(x\) 的信息之后，我们将其从排列中删去。那么我们求 \(L\) 的过程，就是 \(k\) 次向左找到一个最近的没有没删掉的位置，求 \(R\) 的过程与之类似。我们可以用一个路径压缩的并查集来实现一个类似链表的东西。我们先只考虑维护向左的方向，增加一个位置 \(0\) ，初始时所有位置的 \(f[i]=i\)，当我要删除一个位置的时候，就把它并向它左边的位置（合并 \(i\) 和 \(i-1\)），这样我想要找到位置 \(x\) 左边第一个没有被删掉的位置就直接查询 \(find(i-1)\) 就可以了，其中 \(i\) 是 \(x\) 的下标。向右同理。时间复杂度 \(O(nk)\)。

D. Kanade’s trio

题目大意：给出一个长度为 \(n\) 的数列 \(\{A_i\}\)（\(n \leq 5 \times 10^5\)，\(0 \leq A_i <2^{30}\)），求有多少个三元组 \((i,j,k)\) 满足 \(i<j<k\) 并且 \(A_i \oplus A_j < A_j \oplus A_k\)。

题解：考虑如何比较 \(A_i \oplus A_j\) 和 \(A_j \oplus A_k\) 的大小，当然是从高位到低位比较。枚举 \(0\leq len<30\) ，作为两个数最高位相同的位的个数，也即两个数前 \(len\) 位都相同。那么 \(A_i \oplus A_j\) 的第 \(len+1\) 位为 \(0\)，\(A_j \oplus A_k\) 的第 \(len+1\) 位为 \(1\)，就可以确定大小关系了。

可以发现，满足这样条件的 \(A_i\) 和 \(A_k\) 的前 \(len\) 位也都相同，第 \(len+1\) 位不同。两个数在第 \(len+1\) 位的取值取决于 \(A_j\)。\(A_i\) 的第 \(len+1\) 位和 \(A_j\) 相同，\(A_k\) 与 \(A_j\) 相反。

我们可以枚举 \(j\) 和 \(len\) ，去求有多少对 \((i,k)\) 满足 \(i<j<k\) 且 \(A_i\) 和 \(A_k\) 的前 \(len\) 位相同，第 \(len+1\) 位不同，且 \(A_i\) 与 \(A_j\) 的第 \(len+1\) 位相同。

我们先用一个 \(trie\) 来预处理一些信息。从左往右依次插入 \(A_k\)，每次插入之后去 \(trie\) 里询问对于每一个 \(0\leq len<30\)，有多少数满足前 \(len\) 位和它相同，第 \(len+1\) 位与它不同，然后用这些信息去更新 \(f[len][s]\)。\(f[len][s]\) 表示有多少对 \((i,k)\) 满足 \(1\leq i<k\leq n\)，\(A_i\) 和 \(A_k\) 的前 \(len\) 位相同，第 \(len+1\) 位不同，且 \(A_i\) 的第 \(len+1\) 位为 \(s\in\{0,1\}\)。

那么枚举 \(j\) 和 \(len\) 之后，就只需要去询问 \(f[len][s]\)，其中 \(s\) 为 \(A[j]\) 的第 \(len+1\) 位的值。但是这样计算只考虑了 \(i< k\)，还需要删掉不合法的情况。也即 \(i<k\leq j\) 和 \(j\leq i<k\) 的情况。我们可以再用一个 \(trie\) 来维护 \(i<k \leq j\) 的情况，同时在第一个 \(trie\) 中用删除操作维护 \(j\leq i<k\) 的情况。时间复杂度 \(O(n\log{A})\)。

E. RXD and dividing

题目大意：给你一棵边上带权的树，定义函数 \(f(S)\) 表示点集 \(S\) 的最小斯坦纳树。你需要将 \(\{2, 3, \dots, n \}\) 分成 \(k\) 个划分 \(S_1, \dots, S_k\)。\(S_i\) 可以为空。最大化 \(\sum \limits_{i=1}^k f(\{ 1 \} \cup S_i)\)。

题解：考虑每条边 \((u,v)\) 的贡献，其中 \(v\) 是 \(u\) 的儿子，答案就是 \(\mathrm{min}(k, sz_v) \cdot w\)。

F. RXD and functions

题目大意：给你一个 \(n\) 次多项式 \(f(x)=\sum_{i=0}^{n}b_{i}x^{i}\) ，和长度为 \(m\) 的数列 \(a_{i}\) ，求 \(g(x) = f(x-\sum_{i=1}^{m}a_{i})\) 。

题解：设 \(-\sum_{i=1}^{m}a_{i}=a\)：

\[ \begin{aligned}\\ g(x)&=f(x+a)\\ &=\sum_{i=0}^{n}b_{i}\sum_{j=0}^{i}C_{i}^{j}x^{j}a^{i-j}\\ g_{i}&=\sum_{j=i}^{n}b_{j}C_{j}^{i}a^{j-i}\\ &=\sum_{j=i}^{n}b_{j}\frac{j!}{i!(j-i)!}a^{j-i}\\ i!g_{i}&=\sum_{j=i}^{n}j!b_{j}\cdot\frac{a^{j-i}}{(j-i)!}\\ \end{aligned}\\ \]

这玩意儿看起来很像卷积，不过 \(j\) 和 \(j-i\) 是同时增长的，解决这个问题很简单，只要把其中一个数列 reverse 一下就好了，然后 \(NTT\) 加速。复杂度 \(O(nlogn)\) 。

G. RXD and logic gates

题目大意：你有很多个输入为 \((a, b, c)\) 输出为 \((a, b, c\oplus (a\land b))\) 的三输入逻辑门。现在让你用电路模拟一个 \(m\) 元的 bool 关系。电路有 \(m\) 位是输入位，另外有一个输出位，你可以增加 \(t\) 个额外的位。输出位和额外位的初值你定，要求 \(t, n\leq 800\)，其中 \(n\) 是使用的三输入逻辑门的个数。

题解：我们首先分析这个三输入逻辑门，注意到 \(0\oplus (a\land b) = a\land b\)， \(1\oplus (a\land 1) = \lnot a\)。于是我们可以做取反和与操作，显然 \(\{\lnot, \land \}\) 是一个完全集，我们在此基础上继续如下操作。为了后续操作，我们用 \(3\) 个额外位分别表示常量 \(1, 1, 0\)，以及 \(m\) 个额外位来存储 \(\{\lnot x_i \}\)。取反操作可以令初值为 \(1\)，然后输入 \((x_i, 1, \lnot x_i)\) 来完成。

我们首先识别出输入的 \(m\) 位表示的数是 \(0\sim 2^m-1\) 的哪一个。这个操作可以利用 \(2 + 4 + \dots + 2^m = 2^{m+1} - 2\) 个额外的位来完成，分别表示长度为 \(i(1\leq i\leq m)\) 的前缀是否存在，然后递推即可。

根据输入的真值表，我们可以知道输入为 \(0\) 和 \(1\) 的值哪个更少。设 \(\text{out}\) 为这个值，并设该值的自变量取值集合为 \(S\)，有 \(|S|\) 至多为 \(2^{m-1}\)。对这 \(2^{m-1}\) 个变量，记录相应的识别位的取反。设 \(res\) 为集合 \(S\) 中的自变量对应识别位的取反的与。最后通过 \(\text{out} = \text{out} \oplus (\text{ONE} \wedge \text{res})\) 这个操作即可得到答案。

总的额外变量数至多为 \(3 + m + 2^{m+1} - 2 + 2^{m-1} = 5\cdot 2^{m-1} + m + 1\)。操作数至多为 \(m + 2^{m+1} - 2 + 2\cdot 2^{m-1} + 1 = 3\cdot 2^m + m - 1\)。两者都是不超过 \(800\) 的。

H. RXD and math

题目大意：算个式子。

题解： \([1,n^{k}]\) 中的每个整数可以唯一的表示成 \(a = b*c\) 的形式，其中 \(b\) 是一个完全平方数， \(c\) 中没有平方因子。故：

\[\begin{align} \sum_{i=1}^{n^{k}}\mu^{2}(i)\lfloor\sqrt{\frac{n^{k}}{i}}\rfloor &= \sum_{i=1}^{n^{k}}\mu^{2}(i)\sum_{j=1}^{\lfloor\sqrt{\frac{n^{k}}{i}}\rfloor}1\\ &=\sum_{i=1}^{n^{k}}1=n^{k} \end{align} \]

I. RXD and numbers

题目大意：序列 \(\{ A_i \}\) 满足以下性质：

• \(1\leq A_i \leq m\)
• \(A_1=A_n=1\)
• \(\forall 1\leq x \leq m, \exists p, s.t.A_p=x\)
• \(\forall x, y\)，满足 \(A_i=x\; and\; A_{i+1}=y\) 的 \(i(1\leq i < n)\) 的个数为 \(D_{x, y}\)

求满足条件的序列的个数，要求序列的长度 \(n\geq 2\)。

题解：我们从 \(x\) 到 \(y\) 连 \(D_{x,y}\) 条有向边，那么问题变成了求从 \(1\) 开始的欧拉回路个数。注意回路与序列并不是一一对应的，因为序列的值在点上，而不同的回路可能有相同的点序列。

通过 BEST theorem 可知，如果将每条边视为不同，则有向图中本质不同的欧拉回路数量为：

\[ec(G) = t_w(G) \prod_{v \in V}{(\deg(v) - 1)!}\]

其中，\(t_w(G)\) 表示以 \(w\) 为根的树形图个数，这里 \(w\) 可以任选。通过 Matrix-Tree theorem 可知，有向图中以 \(w\) 为根的树形图个数，等于该图对应的基尔霍夫矩阵对于 \(w\) 所在行列的余子式。其中基尔霍夫矩阵等于入度矩阵减去反图的邻接矩阵。

BEST theorem 求出的是不含循环同构的欧拉回路个数。本题中指定 \(1\) 为起点，所以要在上述欧拉回路上选择 \(1\) 的一条边作为开始，并且要将相同的边去重，所求即 \(\displaystyle \frac{deg^{+}(1)ec(G)}{\prod_{u, v\in V} D_{u,v}!}\)。

坑点在于要判断图连通性和是否为欧拉图。

J. RXD, tree and sequence

题目大意：一棵以 \(1\) 为根的树，根的深度为 \(1\)。给你一个 \(n\) 的排列，你需要将排列划分为 \(k\) 段，每一段的价值为 \(lca\) 的深度。求最小的代价和。\(n\times k\leq 3\times 10^5\)。

题解：很容易得到 dp 方程：

\[dp[i][k] = \mathrm{min}(dp[j][k-1] + dep[lca(p_{j+1}, \dots, p_i)])\]

但是直接做复杂度是 \(O(n^2k)\) 的。所以我们考虑用 cdq 分治来优化 dp。考虑用 \(dp[l][j-1], \cdots, dp[m][j-1]\) 来影响 \(dp[m+1][j], \cdots, dp[r][j]\)。

先预处理出 \(a_i(i\leq m)\) 表示 \(lca(p_i, \dots, p_m)\)， 以及 \(a_i(m < i)\) 表示 \(lca(p_{m+1}, \dots, p_i)\)。考虑枚举每一个 \(i\in [m+1, r]\)，然后用前面的来转移到它。需要注意的是 \(lca\) 在到根的一条链上。前面的 \([l, m]\) 可以分成两段，分别预处理前后缀最小值来转移。两段分界点设为 \(fen\)，那么前后的 \(lca\) 可以直接得到。如下图：

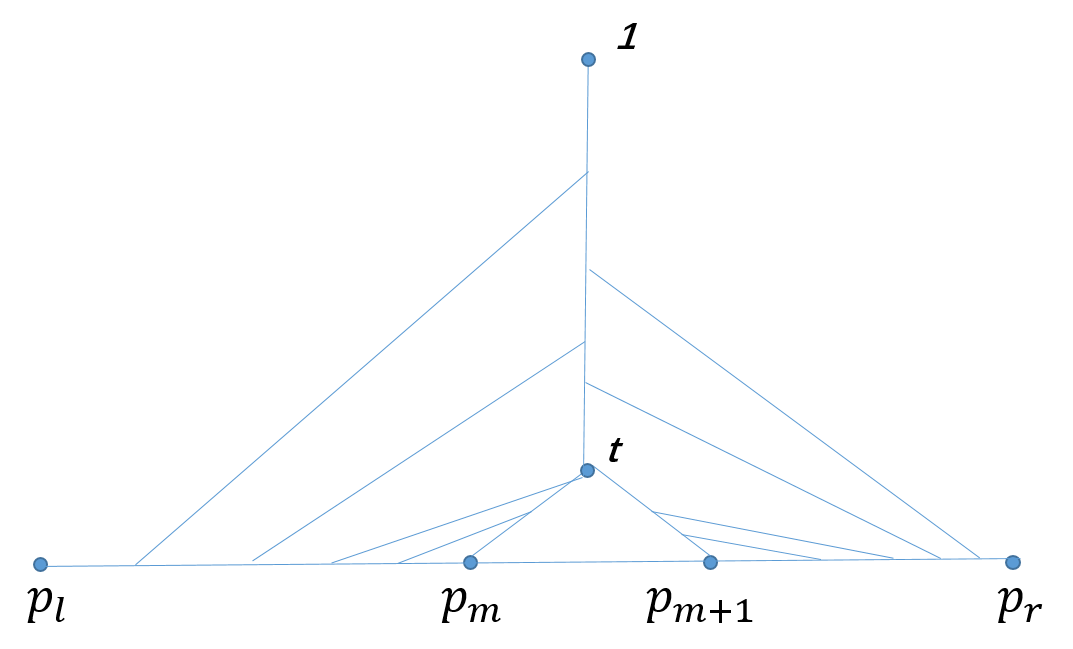
我们先找到 \(t = lca(p_m, p_{m+1})\)，然后让初始的 \(fen\) 满足 \(a_{fen}\) 在 \(t\) 的上方。将右边的 \(j\in [m+1, r]\) 分为 \(a_j\) 在 \(t\) 下方和上方两种情况分别讨论即可。注意到 \(a\) 在两侧都递增，所以 \(fen\) 可以单调移动。时间复杂度 \(O(nklogn)\)。

K. RXD’s date

签到题