Contest Info

date: 2018.01.29 14:00-19:00

practice link

Solutions

B Buffalo Barricades

题目大意：在一个网格上建立平面直角坐标系，每一个格子的坐标用其右上角的点的坐标表示。第一象限的格子中有 \(n\) 头牛，另外有 \(m\) 个人依次以 \(m\) 个点为基点建造栅栏，建造规则是从该基点一直向左向下延伸，直到碰到之前人的栅栏或者碰到坐标轴。保证所有人的基点的横、纵坐标分别互不相同。现在问每个人建造完栅栏时，他围出的那部分有多少头牛。

题解：我们先离线处理出所有人建造完栅栏后，每个人围出的部分有多少头牛，并求出每个人的区域被另外哪个人的区域包含（可能不被包含）。这一部分可以用扫描线完成：将牛和基点一起按照 \(y\) 坐标从大到小排序，注意按照图形的性质， \(y\) 坐标相同时我们要先处理栅栏，再处理牛。我们用一个 set 维护当前 \(y\) 坐标下存在的所有栅栏的 \(x\) 坐标。当扫描线碰到一头牛时，显然它所属的部分是当前 set 中 \(x\) 坐标大于等于它且离它最近的那个（可能不存在）。当扫描线碰到一个基点时，我们先删除掉垂直方向被它截断的那些栅栏。显然这些栅栏是连续的，所以我们可以从当前基点的左边开始依次判断，若碰到的栅栏出现时间比当前晚，那么就可以删除掉该栅栏，否则当前的栅栏被截断，退出循环。显然当前人的区域被当前 set 中 \(x\) 坐标大于等于它且离它最近的那个区域包含（可能不存在），之后我们把当前栅栏加入 set 。

容易发现，每个人建造栅栏时，要么不影响前面人围出的部分，要么恰好将之前的一个部分分成两块。我们逆序处理所有的询问，用一个并查集来维护每一块的 \(\text{size}\)，每次遇到第二种情况时，就将当前区域和它被包含的区域合并。

复杂度 \(\mathcal{O}((n+m)\log (n+m))\) 。

C Cumulative Code

题目大意：给你一棵 \(k\) 阶的满二叉树，从上到下、从左到右从 \(1\) 开始编号，设 \(\{p_{n}\}\) 是它的 \(\text{prufer}\) 序列。给你三个数 \(a,d,m\)，求 \(\sum_{i=0}^{m-1}p_{a+id}\)。

题解：首先我们描述这个问题的递归策略，注意到递归到当前子树时，若当前子树的根上面已经没有东西（即以 \(2^{i}-1\) 为根的子树），那么这个子问题的递归方式为”左子树-根-右子树“，否则为”左子树-右子树-根“。以第一种情况为例，设当前子树的阶数为 \(k\)：首先我们容易求出寻问数列在左子树的部分，这是第一个子问题。然后我们将寻问数列的每一项都减去 \(2^{k-1}-1\) （实际实现时并不会真的减），那么此时根等价于处在 \(1\) 号位置，我们可以判断寻问数列中是否有 \(1\)，来判断是否要加上根对应的值，之后同样的将寻问数列减去 \(1\)，再求出寻问数列在右子树的部分，这是第二个子问题。直接实现的复杂度为 \(\mathcal{O}(2^{k})\)。

我们考虑加上一些预处理。设 \(f_{i,j}(x)\) 表示以 \(x\) 为根的第二种 \(i\) 阶子树的 \(\text{prufer}\) 序列，从第 \(j\) 项开始，每次隔 \(d\) 项的所有项之和，即 \(\sum_{u=0}p^{(x)}_{j+ud}\)。容易证明，这个函数是 \(x,\lfloor\frac{x}{2}\rfloor,1\) 的线性组合。根据上面的递归方式，我们容易 \(\mathcal{O}(1)\) 地求出每个 \(f_{i,j}\) 。我们预处理 \(\displaystyle{f_{1},\cdots,f_{\frac{k}{2}}}\)，时间复杂度为 \(\displaystyle{\mathcal{O}(2^{\frac{k}{2}})}\)。在递归的时候，如果是第二种情况，阶数 \(\le\frac{k}{2}\)，寻问数列又恰好从第 \(j\) 项开始覆盖了每隔 \(d\) 项的所有项，就可以用预处理的结果了。显然利用到预处理结果的次数是 \(\displaystyle{\mathcal{O}(2^{\frac{k}{2}})}\)。与线段树类似，两边不完整的区间只有 \(\mathcal{O}(k)\) 个，第一种情况也只有 \(\mathcal{O}(k)\) 个。

复杂度 \(\displaystyle{\mathcal{O}(2^{\frac{k}{2}})}\)。

Problem D: Donut Drone

题目大意：

​ 有一个\(r\times c(3\le r,c\le2000)\)的网格，每个位置有一个权值\(1\le e_{i,j}\le10^9\)，每个格子\((i,j)\)向\((i+1,j+1)\)，\((i,j+1)\)，\((i-1,j+1)\)三个格子（如果超出网格范围，则循环移动，如第\(n+1\)行实际是第\(1\)行，第\(-1\)列实际是第\(c\)列）中\(e\)最大的一个连一条出边，数据保证任意格子在连边的时候不会出现两个\(e\)相同的备选位置。

有\(m\)次操作，每次操作为如下两种之一：

• 从当前位置（初始为\((1,1)\)）沿有向边走\(1\le k\le10^9\)步到达新的位置，输出新的位置的坐标；
• 修改位置\((a,b)\)的权值为\(e\);

题解：

\(n\)条有向边将所有格子连成了若干环套内向树组成的森林。

用link-cut tree维护每一棵环套树，每棵树的根是环上的某个点。

注意，link-cut tree必须要保证内向树边的方向，不可以进行evert操作（否则无从恢复环上的非树边）；

link之前要先确定两个点不连通。cut之后要尝试link原来环套树环上的那条非树边。

操作一就分为两段，从当前位置所在点走到link-cut tree的根，之后再不断重复在环上走。

分情况，用link-cut tree查询对应splay的kth 即可。

操作二则直接尝试修改\((a+1,b-1)\)，\((a,b-1)\)，\((a-1,b-1)\)三个位置的出边即可。

E Embedding Enumeration

题目大意：给你一棵树，要求你将结点填入一个两行无穷列的网格中，要求点 \(1\) 在左上角，有边相连的结点在相邻的格子中，求方案数。

题解：首先注意到若以 \(1\) 为根，则该树必须是一棵二叉树，否则不存在方案。这是因为结点 \(1\) 在左上角，它的度不超过 \(2\)，而其它点的度也不能超过 \(3\)。我们设 \(dp[u]\) 表示该树只剩 \(u\) 的子树没填，并且 \(u\) 左边的所有列已经不能再填入东西的方案数，如图所示，答案即为 \(dp[1]\)：

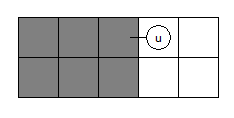
若 \(u\) 没有孩子，则 \(dp[u]=1\)

若 \(u\) 有一个孩子，设为 \(v\)：

• 若将 \(v\) 填入 \(u\) 的下方

  • 若 \(v\) 没有孩子，则 \(dp[u]=dp[u]+1\)。
  • 若 \(v\) 有一个孩子 \(w\)，则 \(dp[u]=dp[u]+dp[w]\)
  • 若 \(v\) 有两个孩子，则不合法

• 若将 \(v\) 填入 \(u\) 的右侧，首先 \(dp[v]\) 代表的所有方案都是合法的，故 \(dp[u]=dp[u]+dp[v]\)，这样做漏掉的情况是 \(u\) 下方填有结点的方案，有如下几种：

  • 若 \(u\) 的子树是一条大于 \(2\) 且长度为偶数的链，则 \(dp[u]=dp[u]+1\)，如图：

  

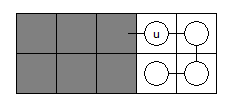
  • 如图所示的情况，\(dp[u]=dp[u]+dp[w]\)：

  

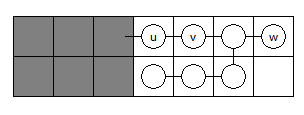
  • 如图所示的情况，也有 \(dp[u]=dp[u]+dp[w]\)：

  

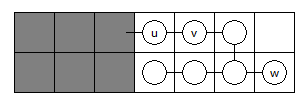
  • 如图所示的情况，\(w\) 和 \(x\) 的子树是长度相等的两条链，此时 \(dp[u]=dp[u]+1\)

  

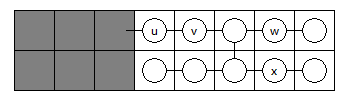
  • 如图所示的情况，\(w\) 和 \(x\) 其中一个的子树是较短的链，另一个在超过较短的链之前（即在结点 \(y\) 之前）保持链的形状，此时 \(dp[u]=dp[u]+dp[y]\)

  

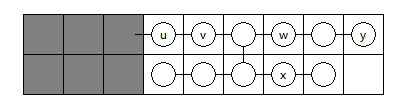
若 \(u\) 有两个孩子，则情况和之前的两种类似，即要么两个孩子的子树是长度相差 \(1\) 的两条链，此时 \(dp[u]=dp[u]+1\)；要么一个孩子的子树是较短的链，另一个在超过较短的链之前保持链的形状，此时 \(dp[u]=dp[u]+dp[y]\)

以上诸如 \(w,y\) 等结点的寻找，可以通过预处理出每个结点的子树是否是链、链的长度，子树中第一个分叉点及到它的距离，均摊 \(\mathcal{O}(1)\) 地计算出来。

复杂度 \(\mathcal{O}(n)\)。

F Faulty Factorial

题目大意：给你三个数 \(n,p,r\) ，其中 \(p\) 是质数，要你将 \(n!=1\times2\times\cdots\times n\) 中的一个数 \(i\) 修改成 \([1,i)\) 中的一个整数（不能不改），使得修改后的乘积模 \(p\) 等于 \(r\) 。求一种方案或判断无解。

题解：分类讨论。

• 若 \(r=0\)

  • 若 \(n<p\) ，无解
  • 若 \(n=p=2\) ，无解
  • 若 \(n=p\) 且 \(p\neq2\)，将 \(2\) 修改成 \(1\)
  • 若 \(n>p\)，将 \(n\) 修改成 \(p\)

• 若\(r\neq0\)

  • 若 \(n<p\)，依次尝试修改 \([1, n]\) 中的每一个数 \(i\)，将其修改为 \(r\cdot(\frac{n!}{i})^{-1}\)，如果它小于 \(i\) ，则是一个合法的解
  • 若 \(p\le n<2p\)，将 \(p\) 修改为 \(r\cdot(-(n-p)!)^{-1}\)
  • 若 \(n\ge2p\)，无解

复杂度 \(\mathcal{O}(p)\) 。

L Lunar Landscape

题目大意：平面上有一些正方形，它们的顶点都是整点，并且它们要么边与坐标轴平行，要么边与坐标轴成 \(45^{\circ}\) 角，求它们覆盖的总面积。所有坐标在 \([-1500,1500]\) 范围内。

题解：由于坐标范围很小，所以我们可以直接对两种正方形分别用二维前缀和求出该种正方形覆盖的情况，对于第二种可以将平面旋转 \(45^{\circ}\) 处理。之后把两种正方形合并起来，我们只需要把原坐标系的每一个格子按对角线分割成 \(4\) 块就能很方便地处理第二种情况了。

复杂度 \(\mathcal{O}(d^{2})\)，其中 \(d\) 为坐标的范围，即 \(3000\) 。