Contest Info

date: 2018.08.26 12:00-17:00

practice link

Solutions

A. Auxiliary Project

签到题。

B. Boolean Satisfiability

签到题。

C. Consonant Fencity

签到题。

D. Dividing Marbles

题目大意：定义 \(m=2^{d_1}+2^{d_2}+2^{d_3}+2^{d_4}(d_i\in[0,20])\)，一开始 \(S=\{m\}\)。每次操作可以选一个 \(m\in S\)，然后把 \(m\) 分成两个正数 \(m_1,m_2\) 的和，然后把 \(m_1,m_2\) 放回集合（不可重）。问你最少多少次操作使得集合 \(S=\{1\}\)。

题解：把操作反过来看就相当于要求 \(m\) 最短的加法链，一种常见的较短的加法链即为快速幂对指数的拆分方法。设 \(m\) 的二进制表示下 \(1\) 的个数为 \(v(m)\)，那么使用快速幂的加法链的长度为 \(\lfloor\log_{2}m\rfloor+v(m)-1\)。另外，设 \(m\) 最短的加法链长度为 \(l(m)\)，\(Knuth\) 猜想 \(l(m)\ge\lfloor\log_{2}m\rfloor+\lceil\log_{2}v(m)\rceil\)，且这一猜想对 \(v(m)\le8\) 已经得到证明。那么 \(v(m)\le3\) 时，显然按照快速幂分解已经取得最优；\(v(m)=4\) 时，有可能比快速幂的长度短 \(1\)，我们可以暴搜出所有这样的数，对于其它数按照快速幂分解即可。

E. Equal Numbers

题目大意：给出一个长度为 \(n\) 的正整数数列 \(\{a_i\}\)。你每次可以选择一个 \(a_i\) 把它变成它的倍数。对于 \(0\leq k\leq n\)，让你输出操作 \(k\) 次之后最少有多少种数字。

题解：把相同的数字缩在一起，然后用两个 vector 分别存所有的数字，以及数列中有自身倍数的数字。把两个 vector 按照数字出现次数排序，然后求出前缀和。对 \(\forall k\)，我们分别找到两个 vector 中前缀和不超过 \(k\) 的前缀 \(i,j\)，设一共有 \(t\) 种数字。那么此时答案为 \(\min(t-(i-1),t-j)\)。

当我们从所有的数字中选择 \(i\) 种数字的时候，把它们都变化到它们的 \(\text{lcm}\)，而这个 \(\text{lcm}\) 是未出现过的数字，贡献是 \(i-1\)；从有自身倍数的数字中选择 \(j\) 种数字的时候，把它们变化到自身的倍数，贡献是 \(j\)。

F. Fygon 2.0

题目大意：给你 \(m\) 个 for 循环，且都是一层一层嵌套的。每层循环有一个唯一的循环变量，下界可以是 1，也可以是一个外层的变量；上界可以是 \(n\)，也可以是一个外层的变量。循环执行时上下界均取到。如果下界大于上界，那么循环不会被执行。分析这段循环关于 \(n\) 的时间复杂度，包括常数。

题解：首先把各个变量的大小关系建成一个有向图，每个 scc 内部必须全取等号。设有 \(k\) 个 scc，那么最后的时间复杂度显然是 \(\mathcal{O}(n^{k})\)。

接下来考虑常数的计算。定义 \(f(n)\) 表示 \(k\) 个变量分别在 \([1,n]\) 中取值，有多少种方案满足这个图的拓扑序，所求即为 \([n^{k}]f(n)\)。注意到如果有两个循环变量相等，那么这部分的复杂度要低于 \(\mathcal{O}(n^{k})\)，不会影响答案。因此不妨将 \(f(n)\) 的定义修改为： \(k\) 个变量分别在 \([1,n]\) 中取值，且互不相等，有多少种方案满足这个图的拓扑序。容易发现，\(f(0)=f(1)=\cdots=f(k-1)=0\)，根据拉格朗日插值公式，\([n^{k}]f(n)=\frac{f(k)}{k!}\)。

考虑 \(f(k)\) 的计算。我们从小到大填入 \(1\sim k\) 中的数，设 \(dp[S]\) 表示 \(S\) 的位置已经被填过，转移很简单。

时间复杂度 \(\mathcal{O}(k\cdot2^{k})\)。

G. Grand Test

题目大意：给出 \(n\) 个点的简单无向图，让你让找两个点 \(s,t\)，和三条从 \(s\) 到 \(t\) 的不相交路径（点不相交且边不相交）。

题解：tarjan。无向图 dfs 树只有树边、反向边和前向边，我们忽略掉前向边。每个点记录 \(\text{low}\) 值和取到 \(\text{low}\) 值的点 \(\text{sit}\)。

如果枚举到树边，那么我们先去 dfs，回溯的时候，考虑 \(\text{low}[v]\) 和 \(\text{sit}[v]\) 是否能跟 \(u\) 构成答案，如果不能，更新 \(\text{low}[u]\) 和 \(\text{sit}[u]\)。

如果枚举到反向边，考虑 \(\text{dfn}[v]\) 和 \(u\) 是否能够跟 \(u\) 构成答案，同样更新 \(\text{low}[u]\) 和 \(\text{sit}[u]\)。

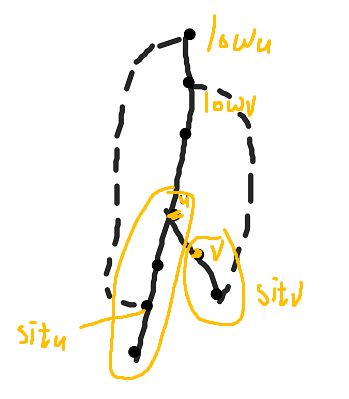
那么三条路径为：

• \(u\rightarrow \cdots \rightarrow \text{low}[v]\)

• \(u\rightarrow \cdots \rightarrow \text{sit}[v]\rightarrow \text{low}[v]\)

• \(u\rightarrow \cdots \rightarrow \text{sit}[u]\rightarrow \text{low}[u]\rightarrow \cdots \rightarrow \text{low}[v]\)

H. Hidden Supervisors

题目大意：给出一棵 \(n\) 个点的有根树森林，其中 \(1\) 所在的树以 \(1\) 为根。让你给其余的树指定根的父亲，使得最后连成的树上匹配最大。

题解：树上最大匹配可以自底向上贪心。我们对森林中每棵树自底向上贪心求出一个最大匹配，这样的最大匹配同时也尽可能使根不被匹配。我们把根已经匹配的树根连向 \(1\)。然后把 \(1\) 号树以外的树，按照树上未匹配点的个数从大到小排序，然后依次把它们连接到 \(1\) 号树上的一个未匹配点，这样会贡献 \(1\) 的匹配，同时我们更新 \(1\) 号树上的未匹配点。

I. Intelligence in Perpendicularia

签到题。

J. Joker

题目大意：给出一个长度为 \(n\) 的不含 \(0\) 的数列 \(\{a_i\}\)，令 \(P\) 和 \(N\) 分别表示正数和负数的和。定义每个位置的权值为 \(w_i=\frac{a_i}{P}\text{ if }a_i>0\text{ and }\frac{a_i}{|N|}\text{ otherwise }\)。定义 \(s_i\) 是 \(w_i\) 的前缀和。现在给出若干组询问，每组询问修改一个位置的权值，然后提问最大的 \(s_i\) 的下标 \(i\)，如果值相同，输出最小的 \(i\)。

题解：记 \(\displaystyle x_i=\sum_{j\le i, a_j > 0} a_j,y_i=\sum_{j\le i,a_j<0}a_j\)，即是要最大化 \(\frac{x_i}{P}+\frac{y_i}{|N|}\)。

按 \(\mathcal{O}(\sqrt{n\log{n}})\) 分块，维护凸包上凸壳，询问时在 \(\mathcal{O}(n/\sqrt{n\log{n}})\) 个凸包上进行三分，修改 \(\text{O}(\sqrt{n\log{n}})\) 重构一块，对一个后缀的块打平移标记即可。

时间复杂度 \(\mathcal{O}(n\sqrt{n\log{n}})\) ，空间复杂度 \(\mathcal{O}(n)\)。

K. Kotlin Island

签到题。

L. Little Difference

签到题。

Dirt Replay

B: -2 W 有点感冒，没想清楚

E: -1 假算法

J: -4 D 有点感冒，不知道在写啥