Contest Info

date: 2018.05.27 09:00-14:15

practice link

Solutions

A Wife

题目大意：给出一个长度为\(n\)的队列，再第\(i\)个位置放1个人的代价为\(a_i\ge0\)，现在要使得任意连续7个位置至少放了7个人，问最小代价为多少？

题解：一定存在一种最优方案，每个位置要么不选，要么选够7个。

B Fund

题目大意：有一种基金的收益计算方法如下：设在第 \(A\) 天买进 \(x\) 元，在第 \(B\) 天全部卖出能够得到 \(\displaystyle{x\frac{v_{B}}{v_{A}}(1-r_{B-A})}\) 元。现在有一个人在第 \(0\) 天时手里有一些钱，现在他准备做一个 \(n\) 天的投资，第一次他会在第 \(1\) 到 \(n\) 天中等概率随机选择一天买进，设为 \(d_{1}\)，然后他会在第 \(d_{1}+1\) 到 \(n\) 天中等概率随机选择一天卖出，设为 \(d_{2}\)，然后在第 \(d_{2}+1\) 到 \(n\) 天中等概率随机选择一天买进。。。每次买进他都会投入手上所有的钱。如果他在第 \(n\) 天买进，那么他会立刻卖出，资金保持不变（即 \(r_{0}=0\)）。求此人第 \(n\) 天后的期望收益率。

题解：设该人开始手中有 \(1\) 元，\(f_{i}\) 表示第 \(i\) 天卖出手上钱的期望，\(g_{i}\) 表示第 \(i\) 天买进手上钱的期望，则有： \[ \begin{aligned} f_{i}&=\sum_{j=1}^{i-1}g_{j}\cdot\frac{1}{n-j}\cdot\frac{v_{i}}{v_{j}}(1-r_{i-j})\\ g_{i}&=\sum_{j=0}^{i-1}f_{j}\cdot\frac{1}{n-j} \end{aligned} \] 其中 \(f_{0}=1\)，答案为 \(f_{n}+g_{n}-1\)。

注意到 \(f\) 右边是一个卷积形式，可以用分治 \(FFT\) 解决，\(g\) 则只需要简单地求一下前缀即可。

本题的难点在于卡常，主要的优化方法包括：

• 使用手写的 complex 代替 std::complex
• 在多项式小的时候暴力乘，常数比 \(FFT\) 小很多，本题实测以多项式次数和为 2e3 为分界线时大致达到最优（可能以次数积做分界线更合理一点？但是对于分治 \(FFT\) 来说两个多项式的次数是成正比的，所以问题不大）
• 使用 myy 的两个 double 数列同时 \(DFT\) 的黑科技，但是这样做会带来较大的精度损失，最终无法通过本题

D Chocolate

题目大意：给出\(n\)个字符串，定义任意两个字符串之间的编辑距离为：从其中一个串中每次操作在任意位置删除或添加一个字符使其变为另一个串所需要的最小操作次数。然后问有多少种划分，使得每个集合满足，集合内任意两个字符串的最大编辑距离（特别地，只包含一个字符串的集合最大距离为0），严格小于，任意集合内部的字符串到任意集合外部的字符串的最小编辑距离。

题解：首先任意两个串的编辑距离就是长度之和减去两倍的最长公共子序列长度

要满足题中的性质，首先要是按照kruscal算法求最小生成树中的某个时刻的局面，但这个条件还不充分

如果某个时刻。连通块a中的所有边都被枚举了， 那么它一定是一个合法的最终局面中可能存在的集合，否则可能必须以更大的连通块的形式出现

对所有边排序做kruscal，顺便用并查集维护连通块大小和块中已经枚举过的边数，合并两个集合时分别判断其是否可以独立出现，是则方案加一

时间复杂度\(O(n^2)\)加上排序复杂度\(O(n^2logn)\)

E Right Angle

题目大意：给出 \(n(3\le n\le240)\)，让你构造一个 \(n\) 个点的简单多边形，让这个简单多边形的 \(90^{\circ}\) 或 \(270^{\circ}\) 角尽可能多。要求不能出现 \(0^{\circ}\) 角或平角，坐标范围 \([0,15]\)，所有点必须为整点。

题解：以 \(n=240\) 为例，构造方法如下：

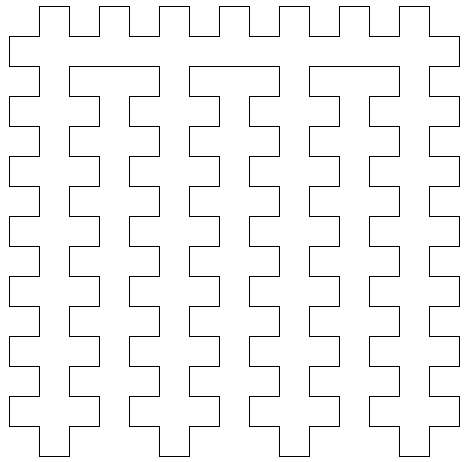
其余情况都可以参照它来构造，\(n\) 为偶数时容易构造出 \(n\) 个直角，\(n\) 为奇数时容易构造出 \(n-2\) 个直角，下面我们证明 \(n-2\) 达到了最大值：

假设有 \(n\) 个直角，那么该简单多边形的内角和为 \(90^{\circ}\times(奇数个1或3的和)\)，显然不是 \(180^{\circ}\) 的倍数，矛盾。

假设有 \(n-1\) 个直角，同理有这 \(n-1\) 个直角的和为 \(180^{\circ}\) 的倍数，那么剩余的一个角也是 \(180^{\circ}\) 的倍数，与不能出现 \(0^{\circ}\) 角或平角矛盾。

F Barber Shop

题目大意：有 \(n\) 个理发师，每位理发师有一个后继（大于他自己的编号，任何两个理发师后继不同）。现在有 \(n\) 位顾客依次来接受服务，每位顾客随机选择一个初始的理发师，如果这位理发师正在服务，就去找他的后继，若编号超过 \(n\) 后都没有空闲的理发师，那么这位顾客就无法接受服务。求所有人都能接受服务的序列数量。

题解：每个理发师向他的后继连一条边（不考虑大于 \(n\) 的点），那么这个图显然是由一些链组成的，容易发现满足条件的一个必要条件是：到每条链接受服务的人数恰等于它的长度。另外我们显然可以先给每一条链固定好分配给它的顾客，这样的方案数为 \(\frac{n!}{\prod sz_{i}!}\)，然后再考虑每条链的合法方案数，它们之间互不影响，即最终答案为 \(\frac{n!}{\prod sz_{i}!}\cdot\prod f(sz_{i})\)。下面我们简要地说明一下 \(f(sz)=(sz+1)^{sz-1}\)：

容易发现一条链能满足顾客要求，当且仅当开始时来到链的最后 \(i\) 个节点的顾客人数不超过 \(i\) 对所有 \(1\le i\le n\) 均成立。这等价于构造一个每个数在 \(\{1,2,\cdots,n\}\) 中取值的长度为 \(n\) 的数列，满足大于等于 \(i\) 的项的个数不超过 \(n-i+1\)。接下来我们说明所有这样的数列与所有 \(n+1\) 个节点的带标号的树一一对应：不妨设这些点为 \(0\) 到 \(n\)，以 \(0\) 为根，我们可以给这个数列赋予如下的意义：\(a_{i}\) 表示 \(i\) 的父亲的 \(bfs\) 序为 \(a_{i}\)，其中 \(bfs\) 序从 \(1\) 开始，\(bfs\) 时同一个结点的所有儿子从小到大遍历。接下来的证明较为容易，这里就不再赘述了。

G Synchronicity

题目大意：给定 \(F_{p}\) 上的 \(n\) 个 \(D\) 维向量，给出两种操作，一种是修改某个位置上的向量，一种是给出两个区间，询问 \(F_{p}^{D}\) 中能被某一个区间线性表示，而不能被另一个区间线性表示的向量数量。

题解：设一组向量张成的子空间为 \(U\)，那么能被它线性表示的向量数量即为 \(p^{\dim U}\)，所以显然我们只需要用一棵线段树维护区间的一组基即可。当然询问操作需要进行一下容斥，设两个区间中的向量张成的子空间分别为 \(U_{1}\) 和 \(U_{2}\)，那么答案为 \(p^{\dim U_{1}}+p^{\dim U_{2}}-2p^{\dim (U_{1}\cap U_{2})}\)，其中 \(\dim(U_{1}\cap U_{2})=\dim U_{1}+\dim U_{2}-\dim (U_{1}+U_{2})\)。

本题有些卡常，常数优化策略包括：

• 合并两组基时，若有一组基满秩，则合并后也必然满秩，不必再计算。
• 合并两组基时，应采用按秩合并的思路，即将秩较小的基合并到秩较大的基上，而不是暴力把两组基并到一起做高斯消元。

H Safe Upper Bound

签到题，输出INT_MAX除以\(n\)最大的质因子，向下取整。

I Number Placement Puzzle

题目大意：使用 \(0\sim K\) 的整数构造一种 \(N\times N\) 矩阵的填数方案，满足：

• 对角线上的元素为 \(0\)
• 若 \(i\) 行 \(j\) 列的元素为 \(x\)，则第 \(i\) 列和第 \(j\) 行均不能出现 \(x\)

求一种方案使得 \(K\) 最小。

题解：设 \(S_{j}\) 表示矩阵第 \(j\) 行所有非对角线元素组成的集合。

首先我们证明任取 \(n\) 个 \(1\sim K\) 组成的互不包含的集合，都能构造出一个符合要求的矩阵：

我们在 \((i,j)\) 处填入 \(S_{j}-S_{i}\) 中的任意一个元素，显然 \(S_{j}-S_{i}\neq\emptyset\)。假设这种填法不满足要求，即存在 \(i\neq j, j\neq k\) 使得 \(S_{ij}=S_{jk}=x\)，即 \(x\in(S_{j}-S_{i})\cap(S_{k}-S_{j})\)，那么显然有 \(x\in S_{j}\land x\notin S_{i}\land x\notin S_{j}\)，矛盾。所以我们构造出了一种符合要求的方案。不妨设 \(\displaystyle{k=\arg\min_{k\in\mathbb{N}}{k\choose \lfloor\frac{k}{2}\rfloor}\ge N}\)，那么我们至少可以构造出一种 \(K=k\) 的方案。

再证明 \(K<k\) 时不能构造出符合要求的方案。显然此时不论如何构造，至少存在一个 \(i\neq j\) 使得 \(S_{i}\subset S_{j}\)。那么 \(S_{ij}\in S_{j}\)，故存在 \(k\neq j\) 使得 \(S_{jk}=S_{ij}\) ，不满足要求。

J Fermat’s Christmas Theorem?

题目大意：求 \(x^{2}+y^{2}\equiv d\pmod N\) 满足 \(0\le x,y<N\) 的解的数量。

题解：首先注意到，根据中国剩余定理，我们可以将 \(N\) 质因数分解后，对每种质因子分别求出答案再乘起来即可。做法为打表找规律+分类讨论。

• \(p=2\) 时
  • 若 \(d\equiv 0\pmod{p^{t}}\) 或 \(d\equiv p^{t-1}\pmod{p^{t}}\)，答案为 \(p^{t}\)
  • 否则设 \(d’\) 为 \(d\) 除 \(p\) 以外的质因子的乘积
    • 若 \(d'\equiv 1\pmod 4\)，答案为 \(p^{t+1}\)
    • 若 \(d'\equiv 3\pmod 4\)，答案为 \(0\)
• \(p\equiv 1\pmod 4\) 时
  • 若 \(d\equiv 0\pmod {p^{t}}\)，答案为 \(p^{t}+t\varphi(p^{t})\)
  • 否则设 \(d’\) 为 \(d\) 除 \(p\) 以外的质因子的乘积，设 \(d=d'\cdot p^{s}\)，答案为 \((s+1)\varphi(p^{t})\)
• \(p\equiv 3\pmod 4\) 时
  • 若 \(d\equiv 0\pmod{p^{t}}\)，答案为 \(p^{2\lfloor\frac{t}{2}\rfloor}\)
  • 否则设 \(d’\) 为 \(d\) 除 \(p\) 以外的质因子的乘积，设 \(d=d'\cdot p^{s}\)
    • 若 \(s\equiv 1\pmod 2\)，答案为 \(0\)
    • 否则答案为 \((p+1)p^{t-1}\)

（证明待续）

K Digital Display for Anniversary

题目大意：有 \(90\) 个数码管，给定初态和终态，给出 \(5\) 种操作：

• 熄灭一个亮着的数码管
• 点亮一个熄灭的数码管
• 熄灭两个亮着的数码管
• 点亮两个熄灭的数码管
• 熄灭一个亮着的数码管，同时点亮另一个熄灭的数码管

问进行 \(T\) 次操作第一次达到终态的操作序列有多少种。

题解：本题关键的性质是：\(1\sim2\) 和 \(3\sim5\) 号操作分别相当于改变一个数码管的状态和改变两个数码管的状态。设 \(dp[i][j]\) 表示 \(i\) 次操作后和终态相同的数码管有 \(j\) 个的方案数，答案即为 \(dp[T-1][1]+dp[T-1][2]\)，矩阵转移即可。注意预处理 \(A^{2^{k}}\) 以降低复杂度。

Replay and Summary

Replay

菜