Contest Info

date: 2018.08.21 12:00-17:00

practice link

Solutions

A. ASCII Addition

签到题

B. Book Borders

题目大意：给出若干个单词，总长度为 \(n\le5\times10^5\)。对于 \(m\le[L,R]\) ，问如果一行只能容纳 \(m\) 个字符（同一行相邻单词之间要有一个空格），每行的第一个单词长度加一的和减去一是多少。

题解：将单词排成一行（相邻单词之间恰有一个空格），预处理出每个位置属于哪个单词，以及每个单词的首字母位置和长度。对于询问 \(m\) ，每次从当前行首字母向后跳 \(m\) 个字符，然后调整到该位置属于的单词的首字母去，\(\mathcal{O}(1)\)。

因为答案的总行数不超过 \(\frac{n}{1} + \frac{n}{2} + \cdots + \frac{n}{n}\) ，时间复杂度为 \(\mathcal{O}(n\log{n})\)。

comment:

本质就是每次直接跳到 \(m\) 长度的位置，然后往回跳一步到单词开头。

C. Cow Confinement

题目大意：一个网格图中有 \(n\) 头牛，\(m\) 朵花和 \(f\) 道篱笆。牛和花在格子中，篱笆在格子的边界上，且篱笆都是长方形。不同的篱笆互不相交，但是有可能嵌套包含。牛可以在网格中向右或向下走，但是不能穿过篱笆，问每头牛分别能走到多少朵花。

题解：定义牛的路径为一直往右走，如果碰到左侧篱笆，就从该篱笆的左下角的下方开始继续往右走；如果碰到右侧篱笆则结束。定义花的路径为一直往上走，如果碰到下侧篱笆，就从该篱笆的左上角的左上方开始继续往上走；如果碰到上侧篱笆则结束。如图：

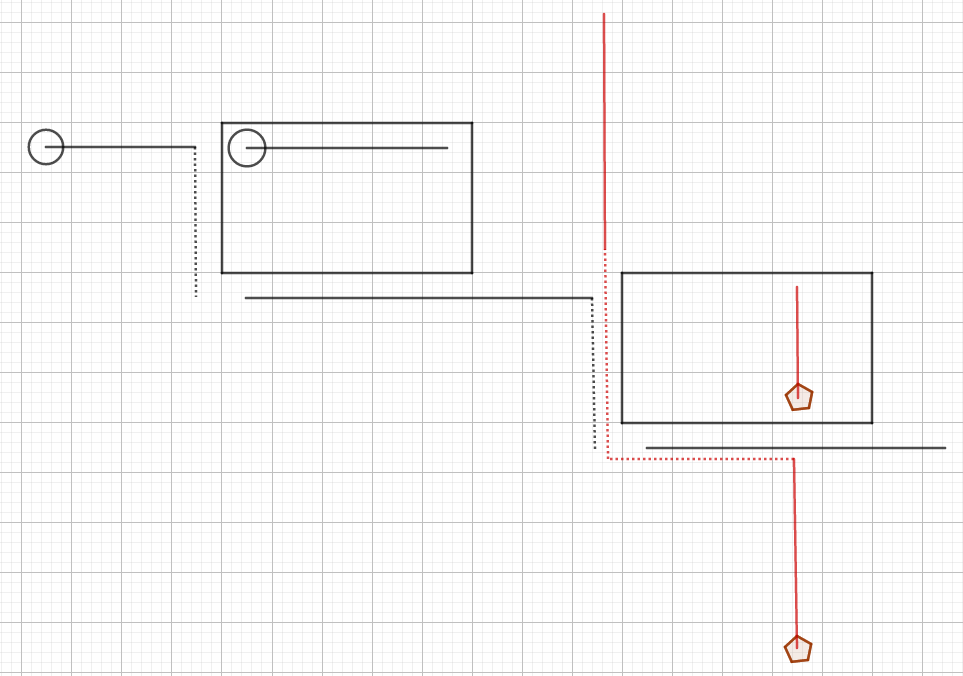
可以证明，一头牛能走到一朵花，当且仅当它们的路径相交，相交时交点有且仅有一个。那么问题就转化为了，统计牛的路径与所有花的路径有多少个交点。

我们先从右往左进行一遍扫描，扫出垂直的花的路径线段，并且将重合的路径合并，重合次数就是它的贡献，容易发现，路径最多只有 \(m+f\) 段。

接着我们从上往下进行扫描线，这个时候就可以计算牛的答案，我们把篱笆左右边界和上面扫出的花的路径线段作为事件，用一个树状数组维护横轴的贡献，那么每次询问就是区间求和。同样的，我们对牛也要进行合并，否则复杂度会不对，对牛合并我们类似虚树合并，然后最后 dfs 一次计算答案。

时间复杂度 \(\mathcal{O}((n+m+f)\log(n+m+f))\)。

D. Digit Division

签到题。

E. Export Estimate

题目大意：给出一个简单边带权无向图，和若干个询问。每个询问给出阈值 \(p\)，要求把原图权值小于 \(p\) 的边删掉，并且删掉孤立点，把度为 \(2\) 的连接不同点的点缩掉，问图的点数和边数。

题解：我们把询问和原图边权从大到小排序，然后依次处理询问。每次先插入合法的边，然后统计度为 \(2\) 的点个数 \(\text{cnt}_2\) 和度为 \(0\) 的孤立点个数 \(\text{cnt}_0\)，以及是一个简单环的连通块个数 \(c\)。我们计算答案的时候只需要把 \(c - \text{cnt}_2 - \text{cnt}_0\) 加到答案里就行了。

F. Frightful Formula

题目大意：给你一个 \(n\times n\) 的矩阵 \(F\)，它的第一行和第一列已经给出。对于其它的格子，有 \(F_{i,j}=aF_{i,j-1}+bF_{i-1,j}+c\)，求 \(F_{n,n}\)。

题解：不妨将两维坐标都减一。容易证明： \[ F_{n-1,n-1}=\sum_{i=1}^{n-1}{n-2+n-1-i\choose n-1-i}a^{n-1}b^{n-1-i}F_{i,0}+\sum_{i=1}^{n-1}{n-2+n-1-i\choose n-1-i}a^{n-1-i}b^{n-1}F_{0,i}+\sum_{i=0}^{n-2}\sum_{j=0}^{n-2}{i+j\choose i}a^{i}b^{j}c \] 对于后面常数项的处理有两种方法：

• 容易看出是一个卷积形式，用拆系数 FFT 优化。
• 令 \(G_{i,j}=F_{i,j}+\frac{c}{a+b-1}\)，消去常数，需要注意处理 \(a+b-1\equiv0\pmod{p}\) 的情况。（并不好处理）

时间复杂度 \(\mathcal{O}(n\log n)\) 或 \(\mathcal{O}(n)\)。

G. Greenhouse Growth

题目大意：给出一个长度为 \(n\) 整数数列和一个长度为 \(m\) 操作序列。每次操作可以选择左或者右。如果选择左，那么从左往右的每一段相同的数字，如果严格小于前一段，那么整段加 \(1\)。选择右的时候，从右往左的每一段相同的数字，如果严格小于后一段，那么整段加 \(1\)。问最后的数列的样子。

题解：我们把相同的连续数字合并，并且用链表维护它们的关系。那么每一段我们可以用一个 \(2\) 位的 mask 来维护它是否被两种操作影响（是否加 \(1\)）。链表中相邻的两项，我们可以提出一个合并的事件（还需要多少次 mask’ 操作，mask’ 是两段 mask 的异或）。

我们依次模拟操作，遇到合并事件就去合并两段，然后更新事件。一段加 \(1\) 可以通过对 mask 打标记进行，我们只需要用当前时刻的 mask 的 cnt 减去该段创建时刻的 mask 的 cnt，就是它加 \(1\) 的次数。

最多有 \(n\) 次合并操作，复杂度 \(\mathcal{O}(n+m)\)。

H. Hovering Hornet

简单几何题，求直线切割凸包的面积。

I. Ice Igloos

题目大意：\(n\) 个半径在 \((0,1)\) 之间的圆，圆心是整点，且坐标范围在 \([1,500]\)，半径只有一位小数。\(q\) 次询问，每次询问给出端点是整点的一条线段，问它与多少个圆有交点。

题解：如果询问的线段是水平或者垂直的，那么答案就是有多少个圆圆心在线段上。否则，我们考虑圆心在哪些位置的圆可能与直线相交，如图：

当线段斜率大于 \(0\) 的时候，矩形 \((x, \lfloor f(x) \rfloor)\) 到 \((x+1,\lceil f(x+1) \rceil)\) 边界上的点均有可能，于是我们枚举这些点进行判断即可。同时注意到，这些点到线段的距离，恰好等于到该直线的距离，大大简化了运算。实现的细节：

• 令线段从 \((x_1,y_1)\) 指向 \((x_2,y_2)\) 的单位方向向量为 \((b,a)\)，那么点到直线的距离为 \(|(x-x_1,y-y_1)\times (b,a)|=|ax-by+by_1-ax_1|\)，令 \(c=by_1-ax_1\)，我们可以预处理 \(a,b,c\) 。

• 对 \(f(x_2)\) 向上取整的时候，可能会有精度误差导致结果为 \(y_2+1\)，此时该点到线段的距离不等于到直线的距离。我们可以在调用 ceil 函数的时候，把参数值减去 1e-6，或者调用 \(f\) 的时候判断如果是 \(x_2\) 直接返回 \(y_2\)。

J. Juice Junctions

题目大意：给出一个无向图，点数 \(n\le3000\) ，边数 \(m\le4500\) ，每个点的度数不超过 \(3\)，每条边的边权都是 \(1\)，求 \(\sum_{i<j} \text{MinCut}(i,j)\)。

题解：首先每个连通块得单独做。因为每个点的度数不超过 \(3\) ，因此最大流不超过 \(3\) ，dinic 最多 \(3\) 次 bfs 就可以求出两个点之间的最小割，这一步是 \(\mathcal{O}(n)\)。使用 Stoer-Wagner 算法可以 \(n-1\) 次 dinic 求出 Gomory-Hu tree ，到这里是 \(\mathcal{O}(n^2)\)。

有了这个树之后，两个点之间的最小割，就是树上路径中的最小瓶颈边，可以将边从大到小排序，然后用并查集再做一次合并，贡献是边权乘以两个连通块大小的乘积。时间复杂度 \(\mathcal{O}(n^2)​\)。

K. Kernel Knights

题目大意：\(2n\) 个骑士，骑士 \(i\) 向骑士 \(f[i]\) 连一条有向边，保证对于 \(\forall i \in [1, n], f[i]\in [n + 1, 2n]\)，对于 \(\forall i \in [n + 1, 2n], f[i]\in [1, n]\)。让你输出一个骑士集合 \(S\)，使得集合内没有两个人有边相连，集合外的骑士均有从 \(S\) 中指出的边。

题解：令 \(S = \{1, 2, \dots, n\}\)，那么有一些点没有被 \(S\) 相连，那么我们把它加进 \(S\)，并且把它指向的在 \(S\) 中的点 \(u\) 删掉，同时删掉 \(u\) 指出的边。用一个队列维护。

std solution:一开始 \(S=\emptyset\)，每次选一个没有入度的点加入集合，黑白染色。不断如此，最后会剩下一个偶环，选一边的即可。

L. Looping Labyrinth

题目大意：一个 \(n\times m\) 的矩形不断在四个方向重复生成无限大的棋盘，每个位置是空地或者墙。给出若干次询问，每次询问无限棋盘中的一个点，问它是否和 \((0,0)\) （初始矩形的左上角）连通。

题解：分三种情况讨论。

• \((0,0)\) 能访问到的点有限，那么这个封闭图形（含边界），一定能被一个大小为 \(n\times m\) 的矩形包住。

• \((0,0)\) 能访问到的点无限，并且能访问的点是一个条带。那么这些条带上的点有一个最小偏移量 \((dx,dy)\)，任意两个在模意义下一样的能访问的坐标，它们之间的偏移都是 \((dx,dy)\) 的倍数。

• \((0,0)\) 能访问到的点无限，并且除了初始的封闭图形，任意点都能访问。

我们从 \((0,0)\) 对棋盘 bfs，第一次访问模意义下的某个坐标的时候，记录真实的坐标。第二次访问的时候，如果此时坐标与真实坐标不一样，那么记录这个偏移量。把偏移量标准化之后去重，然后对输入判断上述三种情况即可。偏移量个数 \(=0,=1,>1\) 分别对应上述三种情况。

Dirt Replay

E: -1 没考虑孤立点

H: -1 排序 x y 写反了