Contest Info

date: 2019.05.02 18:05-23:05

practice link

Solutions

A. Abbreviation

题目大意：给出一段文本，把其中长度两个以上的，满足首字母大写，首字母后跟若干小写字母的单词的，连续序列（相邻单词间有且仅有一个空格隔开）缩写起来输出。

题解：先将文本划分为单词和非单词的极长子段，然后处理一下即可。

B. Binary Code

题目大意：给出 \(n(1\le n \le 5\cdot 10^5)\) 个 0/1 串，串长总和不超过 \(5\cdot 10^5\)。每个串里至多有一个 ?。让你给出一种定 ? 的方案，使得任意两个串不为前缀。

题解：2-sat 问题。

我们把每个串的 ? 取 0 or 1 看作是变量 \(x_i\) 和 \(\lnot x_i\)。我们把定了 0 or 1 之后的两个串，都插入 trie 中，并且在终止节点上保存这个变量。

如果 trie 的每个节点上至多有一个变量，那么我们只需要对于变量，将它与 trie 树上祖先节点上的变量连边即可。每个变量的度是 \(\mathcal{O}(\text{len})\)，其中 \(\text{len}\) 是该变量所在字符串的长度。显然 \(\mathcal{O}(\sum \text{len})\) 是一个合理的复杂度。

如果某个 trie 节点上有大于 \(1\) 个的变量，那么上述复杂度分析不成立，因为该点内部还要连边。注意这些变量只能有一个为 true，那么我们可以用前后缀优化建边。

假设这些变量为 \(x_1, x_2, \dots, x_k\)，那么我们新建节点 \(y_1, y_2, \dots, y_k\)，设外部变量为 \(x\)，连边如下：

 x1     x2     x3    ...     xk
 ↓     ↓     ↓             ↓
 y1 →  y2 →  y3 →  ... →  yk
    ↘     ↘     ↘      ↘     ↘
!x1    !x2    !x3    ...    !xk  !x



!x1    !x2    !x3    ...    !xk
 ↑     ↑     ↑             ↑
!y1 ← !y2 ← !y3 ←  ... ← !yk
    ↖     ↖     ↖      ↖     ↖
 x1     x2     x3    ...     xk   x

C. Cactus Construction

题目大意：定义一种构造 \(n\) 个点的无向图的方法。假设你共有 \(k\) 种不同的颜色可以使用。开始时有 \(n\) 个图，每个图是一个孤立点，颜色为 \(1\)。然后你可以进行有限次如下操作：

• 将两个图合并成一个图，但是不增加新的边
• 将某个图中所有颜色为 \(i\) 的点的颜色变为 \(j\)
• 将某个图中所有颜色为 \(i\) 的点和颜色为 \(j\) 的点（\(i\neq j\)）相互连一条无向边，要求连边之前这两类点之间没有边

使得最后只有一个图（图中点的颜色无所谓）。

现在给了你一棵仙人掌，要求你在 \(k=4\) 的情况下构造出它来。

题解：与之前的某道题类似，我们递归地解决这个问题。

我们任选一个点，目标是构造出该点颜色为 \(1\)，其它点颜色为 \(2\) 的图。

• 如果该点有一条连边是桥，那么我们把桥删去，先把删去桥后的两个连通块构造出来，然后再合并
• 否则该点一定有一条边在一个简单环中，那么我们把这个简单环删去，先把剩下的所有连通块构造出来，然后再合并

有 \(4\) 种颜色的话，合并比较简单。这里就不详细讲了。

D. Delight for a Cat

题目大意：给定 \(n, k, m_s, m_e(1\le k\le n\le 1000; 0\le m_s, m_e\le k; m_s+m_e\le k)\)，让你构造一个长度为 \(n\) 的序列，序列的每个位置是 S 或者 E。满足任意一段连续的长度为 \(k\) 的序列中，S 的个数至少 \(m_s\) 个，E 的个数至少 \(m_e\) 个。还给出序列 \(\{s_i\}\) 和 \(\{e_i\}\) 分别表示位置 \(i\) 取 S 和 E 的收益。要求收益最大。

题解：我们先假设每个位置都是 E，然后设变量 \(x_1, x_2, \dots, x_n\)，\(x_i=1\) 表示该位置取 S，\(x_i=0\) 表示该位置不变，还是取 E。

我们令 \(l = m_s, r = k-m_e\)，列出方程：

\[ \begin{aligned} l&\le x_1+x_2+\dots+x_k \le r\\ l&\le x_2+x_3+\dots+x_{k+1} \le r\\ &\dots\\ l&\le x_{n-k+1}+x_{n-k+2}+\dots+x_n \le r\\ \end{aligned} \]

增加松弛变量，并在前后面加上等式 \(0=0\)：

\[ \begin{aligned} 0&=0\\ x_1+x_2+\dots+x_k &= l + y_1\\ x_1+x_2+\dots+x_k &= r - z_1\\ x_2+x_3+\dots+x_{k+1} &= l + y_2\\ x_2+x_3+\dots+x_{k+1} &= r - z_2\\ &\dots\\ x_{n-k+1}+x_{n-k+2}+\dots+x_n &= l + y_{n-k+1}\\ x_{n-k+1}+x_{n-k+2}+\dots+x_n &= r - z_{n-k+1}\\ 0&=0 \end{aligned} \]

我们做差分，可得：

\[ \begin{aligned} x_1+x_2+\dots+x_k &= l + y_1\\ l + y_1 + z_1 &= r \\ x_{k+1}+r&=l+x_1+y_2+z_1\\ l+y_2+z_2&=r\\ \dots\\ x_n+r&=l+x_{n-k}+y_{n-k+1}+z_{n-k}\\ l+y_{n-k+1}+z_{n-k+1}&=r\\ r &= x_{n-k+1}+x_{n-k+2}+\dots+x_n+z_{n-k+1} \end{aligned} \]

显然上述式子求和为 \(0=0\)，满足流量平衡。我们对每一个等式建一个点，等式左边看作出边，右边看作入边。那么：

• 对于变量 \(x_i\)，我们将它在左边的式子，向它在右边的式子连边，容量为 \(1\)，费用为 \(e_i-s_i\)。
• 对于变量 \(y_i,z_i\)，容量为 \(\infty\)，费用为 \(0\)。
• 对于常量 \(c\)，如果它位于左边，那么它连 \(T\) 容量为 \(c\)，费用为 \(0\)；如果位于右边，\(S\) 向它连边。

最后求最小费用流即可。

E. Expect to Wait

题目大意：有一个租车站，初始时有\(B\)辆车，之后按时间严格递增的顺序有\(n\le10^5\)个事件发生。第\(i\)个事件或者是在\(t_i\)时刻租车站的存库多出\(k\)辆车，或者是\(t_i\)时刻有\(k\)辆车的需求进入队列等待。每当存库和等待队列都不为空时，就会立刻消耗库存中的一辆车来满足队首，这一操作不消耗时间。定义每个需求的等待时间为它进入队列到它被满足之间的时间差，若不能被满足则为无穷大。\(q\le10^5\)次询问，第\(i\)次询问若\(B=b_i\)，那么总的等待时间是多少？

题解：将每一次供应和需求分开考虑，在所有需求都被满足的情况下，总的等待时间等于

\[ \text{供应的时刻之和} - \text{需求的时刻之和} - （\text{供应时供应数大于需求数的供应时刻之和}-\text{需求时供应数大于等于需求数的需求时刻之和}） \] 初始时的\(B\)次供应的供应时刻都为零，可以不考虑它们，需要考虑的就是这\(n\)次事件，显然，\(B\)越大，它们就越可能进入后面的括号中。按事件时间扫一遍求出进入括号时的\(B\)的取值，然后在\(B\)的时间轴上维护一下增量，最后扫一遍\(B\)的时间轴离线回答询问即可。

时间复杂度\(O(n\log{n})\).

F. Foreign Postcards

签到题。

G. Game on Graph

题目大意：有一个\(n\le10^5\)个点，\(m\le2\times10^5\)条边的有向图，允许有自环。\(A\)和\(B\)在图上玩游戏，一开始有一个棋子位于某个顶点上，然后两人轮流操作，每次移动到一个邻点，不能操作的人就输了。显然游戏有三种可能的结果，一种是A胜，一种B胜，一种是不要停下来啊。\(A\)最希望游戏不要停下来，然后希望获胜；\(B\)最希望获胜，否则宁愿输也不希望游戏不要停下来。\(A\)和\(B\)都知道对方的偏好，都采取最优策略，问初始状态在每个顶点时两种先手状态的游戏结果。

题解：先考虑游戏是否能停下来。记录所在顶点和当前的操作者状态， 进行搜索。初始时将没有出边的顶点和任意一人先手入队。然后每次取出队首，如果当前是\(A\)操作，那么上一个人是\(B\)，枚举入边，将没有入队的点都入队；如果当前是\(B\)操作，那么上一个人是\(A\)，枚举入边，如果该点的所有后继节点都是可以停下来的，将其入队。最后没有访问过的状态就是不能停下来的。然后考虑\(B\)是否能获胜，方法和之前的部分一样。然后就只需要先判断是否可以停下来再判断是否是\(B\)获胜即可输出答案。时间复杂度\(O(n+m)\).

H. Hard Refactoring

签到题。

I. Indiana Jones and the Uniform Cave

题目大意：交互题。有一个有向图，点数不超过 \(20\)，但是你不知道有多少个点。每个点有相同数量的出边 \(2\le m\le20\)（已知）。开始时，你在一个随机的点上，每个点的中心有一个石头。每次操作时你需要把这个点的石头放在某条出边的左边和右边，然后再选择一条边走（不一定要和之前那条边一样）。选边的方式是选择相对于石头所在边顺时针多少条边。如果在石头开始时在中间，那么选的边是随机的。之后系统会告诉你你到达的那个点的石头是在中间、左边还是右边。要求你利用这些信息，在 \(20000\) 步内走遍所有的边。保证整个图强连通。

题解：我们利用 \(dfs\) 来搜出所有边，感性的理解一下，这么做唯一的难点就是不能直接回溯，后面会看到如何巧妙地回到上一个点。

我们用 \(\text{left}\) 来表示 \(dfs\) 中已经搜完的点，即 \(m\) 条出边都已经被走过，\(\text{right}\) 表示当前在栈中的点，没搜到的点显然是 \(\text{center}\)。对于 \(\text{right}\) 的这些点，我们用石子表示当前枚举的出边，所以我们只要执行 \(\text{1 right 1}\) 就可以枚举下一条出边。

如果我们走到了 \(\text{center}\)，那么就是找到了一个新的点，我们将当前点和它连边，把它加入栈顶。

如果我们走到了 \(\text{right}\)，说明我们走了一条后向边，如图（灰色的点表示栈中的点，蓝色的边表示当前所走的边）

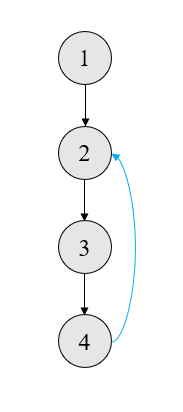
此时，我们将 \(2\) 临时标记为 \(\text{left}\)，即走 \(\text{0 left 0}\)，然后一直沿着当前石子走，即 \(\text{0 right 0}\)。那么当我们再次走到一个 \(\text{left}\) 点时，我们就能够数出走了多少步（这里是 \(3\) 步），从而能知道我们走到了栈里的哪个点。我们建好边，将 \(2\) 还原为 \(\text{right}\)，然后少走一步，就能够“回溯”了。

如果我们走到了 \(\text{left}\)，如图（深灰色的点表示已经搜完的点）

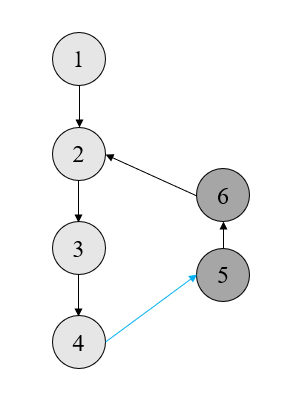
由于 \(\text{left}\) 的点已经搜完，所以它们的所有出边要么还是 \(\text{left}\)，要么是 \(\text{right}\)，而不可能是 \(\text{center}\)。我们可以保证，每个 \(\text{left}\) 结点一直往它的石子方向走，一定能走到一个 \(\text{right}\) 结点（这个后文再说明如何做到）。那么与上一题类似，我们同样可以数出回到了栈里的哪个点。但是遗憾的是，我们不可能知道 \(5,6\) 具体是哪两个点，建图时我们只能让 \(4\) 直接连 \(2\)，后面可以看出这样做没有影响。

当一个点的 \(m\) 条边都已经搜完时，我们需要将它标记成 \(\text{left}\)，并退栈。像之前说的那样，我们要保证把石头放在沿着它走一定能回到栈的道路上。这里我们利用 \(\text{tarjan}\) 求强连通分量的思想，将石头放在 \(\text{low}[u]\)（\(u\) 是当前要退栈的结点）取到最小值的那条出边上。根据 \(\text{low}\) 的定义，我们显然总是可以回到当前的栈中。证明可以采用无穷递降的思想：假设我们永远都走不回栈，那么这条边总是指向 \(dfs\) 树中自己的孩子，由于树的深度是有限的，所以我们总会走到叶子。由于整个图是一个强连通分量，所以必然有 \(\text{low}[u]=\text{low}[\text{leaf}]<\text{dfn}[u]\)，因而这个叶子只能是将石头放在回到栈中 \(\text{low}[\text{leaf}]\) 这个点的道路上，从而矛盾。当然，我们这里只证明了我们能够回到退栈时的栈里，而栈是会不断变化的。不过我们每次都可以保证深度减小，从而最坏情况下也一定可以走到 \(1\)，而 \(1\) 是一定在栈中的。

太 \(\text{nb}\) 了。

J. Jenga Boom

按题意模拟即可。

K. Kids Designing Kids

题目大意：给定了三个 0/1 矩形 \(A, B, C\)，问你是否存在一个偏移量 \((x, y)\)，使得 \(B\) 整个偏移之后，满足 \(A\oplus B = C\)。

题解：也即 \(A\oplus B\oplus C = 0\)，我们考虑每一个矩形的最上然后最左的那个 \(1\)，显然其中的两个要在同一个位置，我们枚举然后 check 即可。

L. List of Primes

题目大意：将所有非空、由质数组成的集合排序，以质数的和为第一关键字，字典序为第二关键字。用 JSON 格式写出这个无限的序列，例如：

[2], [3], [2, 3], [5], [2, 5], [7], [3, 5], [2, 7], [2, 3, 5], [3, 7], [11], [2, 3, 7], [5, 7], [2, 11], [13], [2, 5, 7], ......

求 \([a,b]\) 这个区间的子串。（\(a,b\le10^{18},b-a\le10^{5}\)）

题解：打表可知数据范围内大约只需要 \(2200\) 内的质数，总共有 \(300\) 多个。我们从大到小 \(dp\)，求出 \(dp[i][j]\) 表示所有大于等于 \(i\) 的质数，和为 \(j\) 的方案数及所有方案的 JSON 表示长度之和。预处理的复杂度为 \(2200\times 400\)。这个 \(dp\) 数组包含了求出答案所需的所有信息。

求答案时，一种比较方便的实现方法是类似线段树的递归处理。我们先枚举质数的和，如果该和所占用的区间和 \([a,b]\) 相交，那么就递归下去计算这种情况；然后枚举第一个质数的值，如果相交，就把和减去这个质数，再递归下去枚举第二个质数。。。。。。如果枚举到和为 \(0\) 的情况，就说明我们找到了一个在答案内的集合（为了知道这个集合，需要用栈将之前搜索的质数记录下来）。这一部分的复杂度是 \(\mathcal{O}(b-a)\)。

这样得到的子串会把开头和结尾的“半截”集合补充完整，为了得到正确的答案，我们需要计算一些偏移量，然后在这个串中再截取一下。

M. Mole Tunnels

题目大意：有一棵\(n\le10^5\)个节点的完全二叉树，第\(i\)个节点有\(c_i\)个食物。有\(m\le10^5\)只mole，第\(i\)只位于节点\(p_i\) ，一开始所有的mole都在睡觉。\(m\)次询问，第\(i\)次询问，假设前\(i\)只mole一起醒来，然后出去觅食，经过一些移动后，每个节点上醒来的mole数量都不超过该节点的食物数量，最小化mole移动的距离之和。

题解：可以建出一个最小费用流模型：树边两个方向连流量无穷，费用为\(1\)的边；每个节点向汇点连流量为\(c_i\)，费用为\(0\)的边；源点向每个\(p_i\)连流量为\(1\)，费用为\(0\)的边。如果每次找增广路都找以\(s\to p_i\)开始的，就能得到每个询问的答案。显然这个问题不会有负环，因此，我们只需要维护树上部分的退流。用一个dp来计算子树中向下的流中费用最小的，然后枚举lca，之后再把路径上的退流维护一下，重新计算dp值即可。因为树深度是\(\log{n}\)，因此时间复杂度\(O(n\log{n})\).