Contest Info

date: 2019.07.13 13:41-18:41

practice link

Solutions

B. Fish

题目大意：有 \(n\) 条鱼，每条鱼有一个长度 \(l_{i}\)，和一个颜色 \(c_{i}\)，\(c_{i}\) 是 r,g,b 中的一种。定义一个子集合法，当且仅当集合中任意一条鱼的长度小于另一条的 \(2\) 倍。定义两个合法子集不同，当且仅当两个子集中某种颜色的数量不同。求合法子集的数量。

题解：枚举集合中最短的鱼，可以得到 \((r,g,b)\) 在一个过原点的长方体内取值。因此我们就是要求 \(n\) 个过原点的长方体的体积并。扫描线一维，不妨设为 \(r\)，容易发现 \(g,b\) 两维是阶梯型。如果我们事先把完全被包含的矩形去掉，就可以很容易地用 set 维护答案。

C. JOI Flag

暴力复杂度就对。

E. Rotate

题目大意：\(n\times n\) 的字符正方形，\(q\) 次操作，每次选择一个子正方形逆时针旋转90度。

题解：链表，每个点拆成四个，用一个 go[] 数组记录。复杂度 \(O(nq)\)。

code

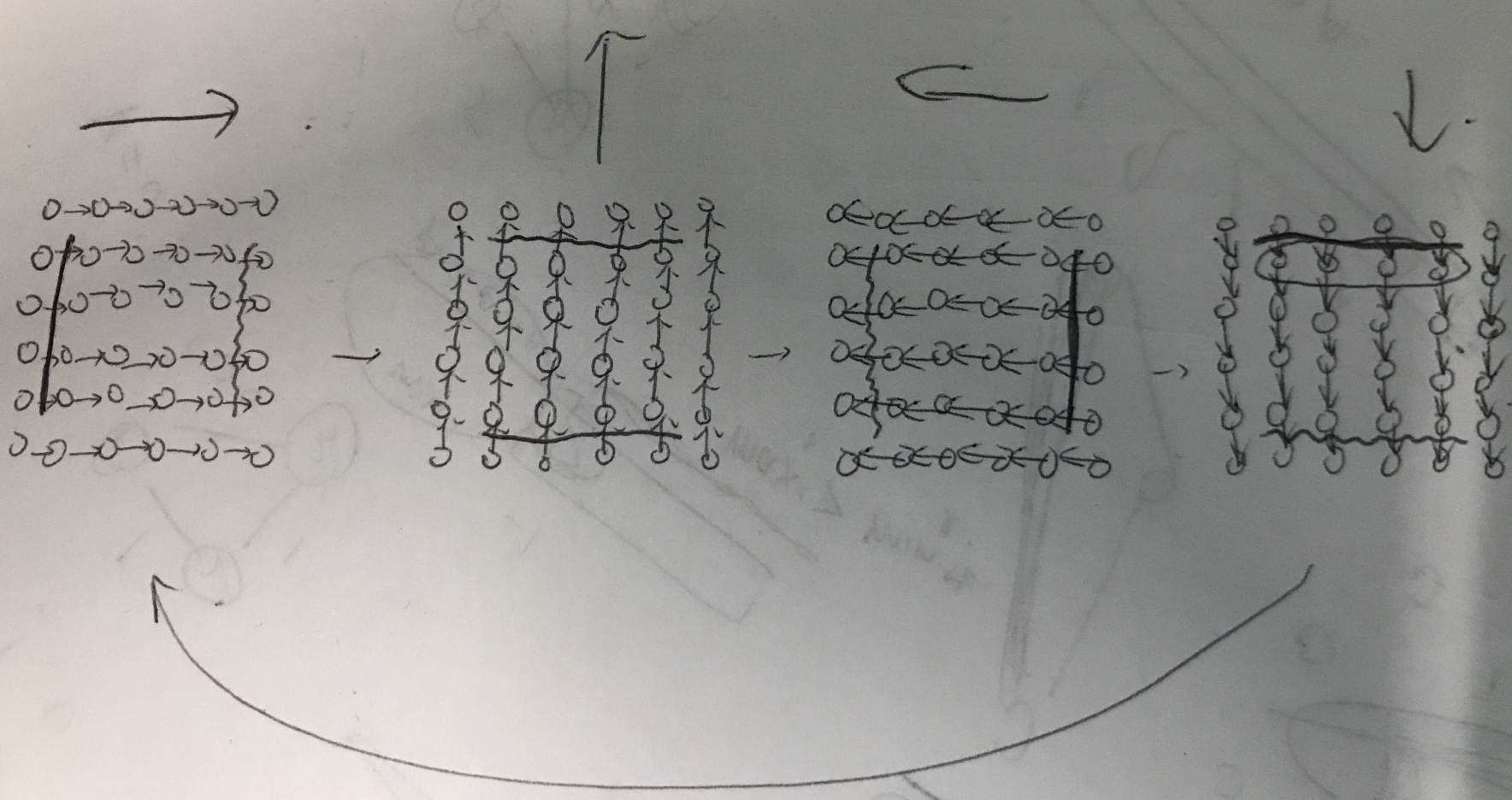
H. Sokoban

题目大意：玩推箱子游戏。已知的有障碍的位置和终点的位置；人和箱子各有一个，但是不知道在哪。问人和箱子有多少种可能的位置使得游戏有解。

题解：我们可以把推箱子的过程建图。注意到人只有在箱子旁边才能推，因此总点数只有 \(4nm\)。人的操作可以是推动箱子，也可以是绕到箱子的剩下三个邻点之一。要支持第二种操作，就必须要快速知道删掉箱子所在的点后，两个邻点的连通情况。最后求答案时，我们也要求出删掉箱子后某个连通块的大小。

为支持这两种查询，我们可以求出点双，建出圆方树，容易知道删一个点的情况下，圆方树的连通性和原图等价。在树上做上面的查询求求 lca 就行了。

时间复杂度 \(\mathcal{O}(nm\log nm)\)。

I. Chinese

太烦了不想写。总之就是贪心解决，然后用单调队列加速。

J. Invitation

题目大意：有 \(A\) 只狗和 \(B\) 只猫，以及 \(n\) 个 group，第 \(i\) 个 group 包含了 \([p_{i},q_{i}]\) 之间的狗，\([r_{i},s_{i}]\) 之间的猫，价值为 \(t_{i}\)。一开始邀请了狗 \(C\)。然后对于每一只未被邀请的动物，计算它所在的 group 中，已有动物被邀请的那些 group 价值的最大值，作为它当前的 happiness。然后邀请 happiness 最大的动物，如果相同，狗优先于猫，如果还有相同，位置小的优先。求每次邀请动物的 happiness 之和，或判断不可能邀请完。

题解：首先离散化，然后用线段树维护所有动物的 happiness。一个动物被邀请后，把 happiness 置为 \(-\infty\)。虽然线段树支持的操作是区间取 \(\max\)，但是由于我们取出这个动物后就会把所有它属于的 group 更新完，因此之后这个点就不会再操作了。

求出所有包含当前点、且未操作过的 group 不是很容易。我们用线段树维护这样的信息：每个结点用 vector 保存包含当前区间的所有 group。这样所有 vector 的 size 和是 \(\mathcal{O}(n\log n)\) 的。查询时，我们只需要取当前结点到根路径上的所有 group 来操作，并把这些结点清空。事实上我们并没有删干净所有该删的 group，因此我们还需要记一个 vis 来辅助判断。但是由于所有 vector 的 size 只有 \(\mathcal{O}(n\log n)\)，这一部分的复杂度最多也只有 \(\mathcal{O}(n\log n)\)。

时间复杂度 \(\mathcal{O}(n\log n)\)。