Contest Info

date: 2019.03.01 18:03-23:03

practice link

Solutions

A. Digits Are Not Just Characters

签到题。

B. Arithmetic Progressions

题目大意：给你一个长度为 \(n\) 且互不相同的数列，要求你用这些数组成一个等差数列（顺序可以交换），且长度尽可能大。

题解：排序后对每个位置维护每种公差对应的最大长度即可。

都 9102 年了，出题人会卡 unordered_map 了，还是尽可能想一点更好的实现方法。

时间复杂度 \(\mathcal{O}(n^{2})\)。

C. Emergency Evacuation

题目大意：有一辆车，总共 \(r\) 排，有一条过道，两边分别有 \(s\) 个座位。现在某些位置上有人，他们要下车，每一步，不靠过道的座位上的人可以向过道移动一个位置；靠过道的座位上的人可以移动到该排的过道；某排过道上的人可以移动到下一排的过道；靠出口那一排过道上的人可以出去。移动的前提是该位置上没有人，或者这个人也要移动；如果多个人可以移动到同一个位置，只能有一个人移动。问最快多少步所有人能下车。

题解：贪心即可，只要能移动就移动。唯一出现多个人可以移动到同一个位置的情况就是两边靠过道的位置都有人，这时谁走到过道都是一样的。

实现时用 bitset 维护每一行过道是否空闲的信息。

时间复杂度 \(\displaystyle{\mathcal{O}(\frac{r^{2}s}{64})}\)。

D. Shortest Common Non-Subsequence

题目大意：给出两个 01 串 \(s_1\) 和 \(s_2\) ，求长度最短，多个时字典序最小，的 01 串 \(t\) ， \(t\) 既不是 \(s_1\) 的子序列，也不是 \(s_2\) 的子序列，\(1\le|s_1|,|s_2|\le4000\)。

题解：假如已知串 \(t\) ，贪心判断其是否为串 \(s\) 的子序列的方法是，从第一个位置开始，每一次选当前位置最近的一个可以与 \(t\) 匹配的位置匹配，如果这样都无法匹配，则 \(t\) 不是 \(s\) 的子序列。假设字符串下标从 \(1\) 开始，令 dp[i][j] 表示在两个串分别从（含） \(i\) 和 \(j\) 开始匹配时的最小长度，令 \(n+1\) 和 \(m+1\) 为失配位置，则 dp[n+1][m+1] = 0 ， dp[0][0] 是答案。我们从后往前求出 dp 值，然后从状态 \(\{0,0\}\) 开始贪心枚举转移，得到字典序最小的答案。时间复杂度 \(\mathcal{O}(nm)\)。

E. Eulerian Flight Tour

题目大意：给定一个 \(n\) 个点 \(m\) 条边的无向图。让你构造一种加边的方案，使其成为一个欧拉图。

题解：我们分为两步来做：

1. 将每个点的度数变成偶数。

法一：对补图的每条边编号，将其是否被选择设为未知数 \(x_i\)，那么我们可以对每个点建立一个方程。高消即可，复杂度 \(\mathcal{O}(\frac{n^4}{64})\)。

法二：dfs 补图的生成树森林（dfs 森林），如果儿子是奇数点，那么加上它到我的这条边。如果最后根为奇数点，无解。复杂度 \(\mathcal{O}(n^2)\)。

2. 将整个图连通。

• 如果整个图已经是一个连通块，那么找到解。

• 如果连通块个数大于 \(2\)，那么我们从每个连通块中取出一个点，把它们连成一个环。

• 如果连通块个数等于 \(2\)。

  • 如果两个连通块的点数都大于 \(2\)（不可能等于 \(2\)），那么我们各取两个点，连成一个完全二分图。

  • 如果存在一个连通块只有一个点 \(p\)，我们在另一个连通块中找到不相连的两个点 \(u, v\)。将它们连成一个环。如果是另一个连通块是 \(K_{\text{odd}}\)，那么无解。
    • 此时无解可能是第一步中加边的方案所致，所以我们尝试找到两个用新加边相连的点 \(u, v\)，删掉边 \((u,v)\)，连接 \((p, u), (p,v)\) 即可。

F. Fair Chocolate-Cutting

题目大意：给你一个凸包，定义 \(S\) 为所有将它分割成等面积两半的线段集合，求 \(S\) 中线段的最大和最小长度。

题解：我们来研究长度什么时候取到极值。对于至少经过一个顶点的线段，我们可以暴力更新答案，这里不讨论。

对于不经过任何顶点的线段，这里假设顶点所在的边不平行。平行时也可类似处理。

如图，延长 \(AB\) 交 \(DC\) 延长线于 \(F\)。设 \(GF=a\)，\(HF=b\)，\(GH=c\)，\(\angle F=\theta\)。

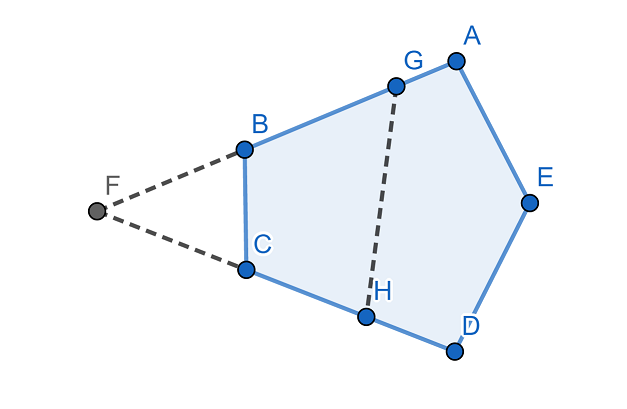
我们有 \(c^{2}=a^{2}+b^{2}-2abcos\theta\)。而注意到 \(S_{GFH}=S_{GBCH}+S_{FBC}\) 为定值，又有 \(S_{GFH}=\frac{1}{2}absin\theta\)，因此 \(ab\) 是定值。由基本不等式，我们很容易知道，\(a=b\) 时，\(c\) 取极小值；并且 \(c\) 没有极大值。

实现时 two pointer 即可。

时间复杂度 \(\mathcal{O}(n)\)。

G. What Goes Up Must Come Down

题目大意：给定一个长度为 \(n\) 的数列，一次操作为交换两个相邻的数。问最少操作多少次，使得存在一个位置 \(k\)（\(1\le k\le n\)），满足 \(a_1,\dots,a_k\) 单调不降，\(a_k,\dots,a_n\) 单调不增。

题解：把所有数字从小到大排序。然后依次考虑，每次把它往左放，或者往右放。往左放的代价，是原位置左边还未放的数字个数，用 Fenwick Tree 维护一下；往右放同理。

实现的时候，每次考虑同一种数字，比较最左一个位置往左放的代价，和最右一个位置往右放的代价。

H. Four-Coloring

题目大意：给你一个平面图，每条边与坐标轴成的角都是 \(45^{\circ}\) 的倍数。给该平面图四染色。

题解：这个平面图的度数最小的点不超过 \(4\)。考虑最上最右的点，它至多只有 \(4\) 条边。我们把它删去之后递归地做这个问题。如果它周围的点至多只有 \(3\) 种颜色，那么直接染就行了。否则我们将它的四条边极角排序。不妨设按极角序的四个点分别为 \(1,2,3,4\)，它们的颜色也分别是 \(1,2,3,4\)。假如我们能从 \(1\) 号点开始，按照颜色为 \(1-3-1-3-\cdots\) 的顺序交替走到 \(3\)，那么 \(2\) 号点必然不能按照类似的方法走到 \(4\)（否则就不是个平面图了）。那么对于不能走到的那条路径，我们把所有按照上述规则能走到的点颜色 swap 一下即可，这样就给我们选择的点匀出了一种颜色。

时间复杂度 \(\mathcal{O}(n^{2})\)，常数很小。

I. Ranks

题目大意：给你一个 \(\mathrm{F}_{2}\) 下的矩阵 \(A\)，定义 \(A^{ij}\) 为 \(A\) 的第 \(i\) 行第 \(j\) 列加一，其它位置不变得到的矩阵。对每个 \(1\le i\le n,1\le j\le m\)，求 \(A^{ij}\) 的秩。

题解：类似于求逆元，我们对 \((A\;I_{n})\) 高斯消元，但是只处理到 \(A\) 的最后一列。高斯消元时要注意使得每个基的第一个 \(1\) 为该列的唯一一个非零元素，例如 \(\left(\begin{matrix}1&1\\0&1\end{matrix}\right)\) 应当变换为 \(\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\)。记处理后的矩阵为 \(B\)。

容易发现，\(A^{ij}\) 经过我们高斯消元的一系列初等行变换后，变为了 \((B_{1}\;B_{2}\;\cdots\;B_{j-1}\;B_{j}+B_{i+m}\;B_{j+1}\;\cdots\;B_{m-1}\;B_{m})\)，因此它们的秩是相等的。我们来考虑加上 \(B_{i+m}\) 后，\((B_{1}\;\cdots\;B_{m})\) 的秩（设为 \(r\)）发生了什么样的变化。

为了方便，我们把 \(B_{j}\) 移到最后一列。

如果 \(B_{j}\) 不含有任意一行的第一个 \(1\)，那么移动后仍是一个阶梯形矩阵。易知不论 \(B_{i+m,1},\cdots,B_{i+m,r}\) 取什么值，都不会影响秩；而如果 \(B_{i+m,r+1},\cdots,B_{i+m,n}\) 中至少有一个非零，那么秩会加 \(1\)。

如果 \(B_{j}\) 含有某行的第一个 \(1\)，那么我们首先要把这一行向下移动，使得矩阵仍为阶梯形矩阵。“每个基的第一个 \(1\) 为该列的唯一一个非零元素”保证了在这里只需要交换行即可得到阶梯形矩阵，而不需要使用两行相加的行变换（可以自己画一下）。如果该行有至少两个 \(1\)，那么情况与上面完全相同。

如果该行只有一个 \(1\)，首先我们注意到，这一行必然被移动到第 \(r\) 行。这种情况与之前的区别在于，如果\(B_{i+m,r}=1\)，那么第 \(r\) 行的基就被异或掉了。考虑这个情况后，剩下的部分也与之前相同。

J. Colorful Tree

题目大意：给出一棵树，每个点有个颜色。若干次操作，或者修改一个点的颜色，或者询问一种颜色的点的虚树周长。

题解：直接每种颜色用一个 set 维护 dfs 序，虚树周长就等于相邻两个点的距离和（加首尾）的一半。时间复杂度 \(\mathcal{O}(n\log{n})\) 。

K. Sixth Sense

题目大意：给出两个长度为 \(n\) 的序列 \(a_1,\dots, a_n\) 和 \(b_1,\dots, b_n\)。要求你把序列 \(b\) 重新排列，使得 \(\sum_{i=1}^n [a_i<b_i]\) 最大，其次 \(b\) 字典序最大。

题解：先考虑如何求最大的 sum。我们把两个序列分别排序，然后用 two point 维护，对于每个 \(a_i\)，贪心的选择最小的比它大的 \(b_j\)。

然后我们考虑让字典序最大，同时保持最大的 sum 可以取到。我们按照输入顺序，依次枚举 \(a_i\)。在排序之后的 \(b'\) 中找到恰比它大的位置 \(j\)，设现在 \(b'\) 的长度为 \(m\)。那么我们可以在区间 \([j, m]\) 中二分，使得 \(a_i\) 和这个数配对，产生 \(1\) 的贡献之后，剩下的数字仍能达到最大的 sum。

否则，我们在区间 \([1, j)\) 中同样二分，但是此时不产生贡献。注意从 \(b'\) 中删掉最后二分出的数字，同时在 \(a'\) 中给 \(a_i\) 打上删除标记。

复杂度 \(\mathcal{O}(n^2\log n)\)。