The 2016 ACM-ICPC Asia Hong Kong Regional Contest
Contest Info
date: 2018.10.03 12:35-17:35
Solutions
A. Colourful Graph
题目大意:给出一个图 \((n\le100)\),和 \(k\) 种颜色。要求用不超过 \(20000\) 次操作将该图的一种染色方案变换到另一种染色方案。其中每次操作是指对于每个点 \(x\),有变换后 \(C'(x)=C(x)\) 或 \(C'(x)=C(y)(\langle x,y\rangle\in E)\)。
题解:假如目标图中有某种颜色原图不存在,那么无解。
注意到一次操作中我们可以交换相邻两个点的颜色。那么对于每种数量少了的颜色,我们可以把它交换到某个数量多了的颜色旁边,再通过一次操作把它覆盖。这样就可以使原图和目标图的颜色数量相同。
同时注意到我们容易用交换相邻点实现交换任意两个点。那么我们只需要依次将点 \(1,2,\cdots,n\) 交换为正确的颜色即可。
B. Doors
题目大意:给你一个图形,问能通过的半径最大的圆是多大。
题解:求出线段之间的距离即可。
C. Playing with Numbers
题目大意:给出 \(n\) 个形如 \(2^{a}3^{b}\) 形式的数,对于每个 \(k\),求出做 \(k\) 次 \(\gcd\) 和 \(n-1-k\) 次 \(\text{lcm}\) 最终得到数的最大/最小值。
题解:以最大值为例。显然若 \(k=n-1\),答案已经固定;若 \(k<n-2\),那么 \(2\) 和 \(3\) 指数上的最大值分别都能取到。
若 \(k=n-2\),显然最后一次做 \(\text{lcm}\) 最优,我们枚举结果中 \(2\) 的幂次贪心即可。
D. Peak Tram
题目大意:给定 \(n\leq 70\) 个建筑物的高度 \(p_i\),定义一个建筑物是可见的,当且仅当它是前缀的严格最大值。要求至少有 \(k\) 个物品是可见的。改变一个建筑物高度为 \(h_i\) 的代价为 \(|h_i-p_i|\times c_i\),求最小代价。
题解:有效的高度为 \(p_i\pm 70\),一共 \(2n^2\) 种。dp 即可,令 \(\text{dp}[i][j][k]\) 表示前 \(i\) 栋建筑,可见 \(j\) 栋,且最高的一座为 \(k\) 高度的代价。转移的时候,枚举 \(i\) 要或者不要,注意不要的时候如果它可见,那么要把它的高度改小。时间复杂度 \(\mathcal{O}(n^3)\)。
E. Peak Tower
题目大意:有 \(n\) 个矩形在平面上做匀速直线运动。求 \([0,t]\) 的时间内,它们并的最小面积(在某个大矩形内)。
题解:把所有线段两两开始相交及结束相交的关键时刻求出来。相邻的两个关键时刻之间,脑补一下应该是一个二次函数,可以三分。
时间复杂度 \(\mathcal{O}(n^{4}\log n)\) 或 \(\mathcal{O}(n^{3}\log^{2}n)\)。
F. Perfect k-ary Tree
题目大意:
给出一棵\(n\le 10^5\)的树,问有多少个子图是完全\(2\le k\le5\)叉树,取模。
题解:
令\(dp[u][j]\)表示\(u\)为根,高度为\(j\)的完全\(k\)叉树个数,考虑点分治求解。
对于当前的分治中心,以它为根进行\(dp\),转移时维护前\(i\)个儿子选出\(k\)个高度为\(j-1\)的完全\(k\)叉树的方案数即可。
当删去分治中心的时候,给它连着的所有未处理的点加一条边连向新增的点,这个点记录分治中心不适用这个子树时的\(dp\)信息,维护转移的前后缀即可快速求得。
新增点数不超过\(n\)个,并且都是叶子,不影响复杂度。
时间复杂度\(O(kn\log^2{n})\).
coldwater’s comment
还可以用换根的树 dp。第一次以 1 为根 dfs 求出 dp1[u][i] 表示以 u 为根的深度为 i 的 k 叉完全树的方案。第二次 dfs 的时候,对于每个点 u,每个深度 h,求出 pre[i][j] 表示前 i 个儿子中选 j 个的方案数,suf 表示后缀(含父亲,用 dp2 计算)。那么可以用 pre 和 suf 求出对于每个儿子 v,它为根的时候,父亲 u 的方案数 dp2[v][i]。
G. Scaffolding
题目大意:
要搭建\(n\le10^5\)列脚手架,第\(i\)列放\(a_i\)个脚手架,每次可以携带\(m\)个脚手架,并且只能在脚手架上左右移动或向上移动,最小化跑的次数。
题解:
可以考虑倒着进行,每次拆最多\(m\)个。
显然高的位置要优先处理,如果某次足够拆掉高的,可以在这一次顺便先拆较低的。
以原数组下标作为平衡树键值,高度作为堆键值(小根堆)建立笛卡尔树。
在笛卡尔树上自底向上贪心,令\(f[u]\)为将\(u\)子树(对应原数组的一个区间)拆到和父亲高度相同的最小次数,\(g[u]\)为在这个条件下可以帮较低的多拆多少个。
那么\(f[u]\)就包括左右儿子已经使用的次数,以及剩下要拆的数量(减去左右儿子帮忙拆的)除\(m\)向上取整,\(g[u]\)就是\(f[u]\cdot m\)减去实际拆掉的数量。
时间复杂度\(O(n)\).
H. Slim Cut
题目大意:给定一个带权无向图 \(G(V,E;w)\)。定义一个割是点的一个划分,把点集划分为两个非空集合 \(S\) 和 \(\bar{S}\)。定义割 \(\{S, \bar{S}\}\) 的 \(\text{slimness}\) 为:
\[ \displaystyle \frac{\displaystyle \max_{(u,v)\in E, u\in S, v\in \bar{S}}w(u,v)}{\min(|S|,|\bar{S}|)} \]
最小化 \(\text{slimness}\)。
题解:枚举最大的割边,那么大于枚举值的边形成了若干个连通块。我们希望这些连通块尽可能均匀地分在 \(S,\bar{S}\) 中,做一个 0/1 背包 dp 即可。
注意到加一条边的时候,实际上是 \(\text{sz}(u)\) 和 \(\text{sz}(v)\) 变成了 \(\text{sz}(u) + \text{sz}(v)\)。也即删除和添加物品的背包 dp。我们可以维护每个物品存在的时间区间,然后对时间分治。那么现在就只有添加操作,再用 bitset 优化背包 dp 即可。
时间复杂度 \(\mathcal{O}(n\log m\times \frac{n}{w})\)。
zhongzihao’s comment
这种背包还可以用多项式来维护。增加一个大小为 \(i\) 物品相当于乘上 \(1+x^{i}\),删除则相当于除以 \(1+x^{i}\)。这两种操作都容易 \(\mathcal{O}(n)\) 做到。因为答案太大,所以要模一个大质数。时间复杂度 \(\mathcal{O}(nm)\)。
I. Special Tour
题目大意:一个 \(n\times m\) 的网格图,要求你构造一条哈密顿回路,使得每条边连接的两点的曼哈顿距离为 \(2\) 或 \(3\)。
题解:不妨设 \(n\le m\)。解题的关键思路是:先构造出一些链,再将这些链连接起来。下面会多次用到这样的方法。
若 \(n=1\),如下的边是必须要连的:
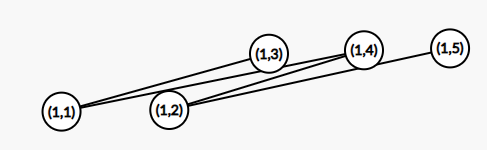
另一侧的 \(m,m-1,\cdots\) 也同理。因此在 \(m<10\) 时,只有 \(m=5\) 有解(把 \((1,3)\) 和 \((1,5)\) 连起来)。
\(m\ge10\) 时,我们从 \((1,3)\) 向 \((1,6)\) 连一条边,右侧也对称地连。之后我们再依次连接 \((1,5)-(1,7),(1,6)-(1,8),\cdots\) 就能将左右两条链拼接在一起了。
若 \(n=2\),\(m=2\) 时是无解的。否则我们可以连成这样:
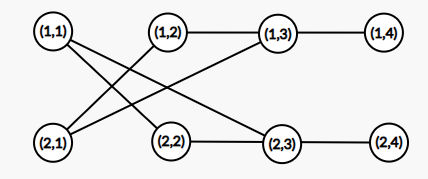
当 \(m\) 更大时可以类似上面那种情况从 \((1,3)\) 每隔两个向后连。之后我们连接 \((1,3)-(2,4),(1,4)-(2,3)\) 即可。
若 \(n,m\) 中有一个为 \(4\),不妨设 \(n\) 为 \(4\)。我们首先连出两个 \(n=2\) 的情况,再对右侧 \(8\) 个点如图所示连接即可:
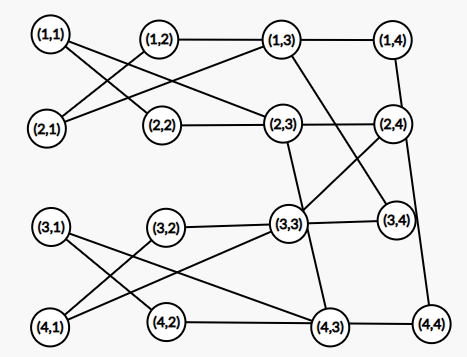
若 \(m\ge6\),那么我们先将每一层按照 \(n=1\) 只连一侧的方式连接起来,右边两列随便画一下就能连接起来(懒得画图了)
剩下 \(n=3,m=3\),\(n=3,m=5\) 和 \(n=5,m=5\) 的情况,手动打表即可。
J. Taboo
题目大意:
给出\(n\)个\(01\)串,求一个最长的不包含这\(n\)个串为子串的\(01\)串,若无限长输出\(-1\),若多解输出字典序最小的。
题解:
建立\(Trie\)图,删去不合法的状态(终止节点,以及它在trie树上的子树,以及在fail树上的子树),若不是\(DAG\)则可以无限长,否则正反两次求最长链,从根开始枚举字典序最小的答案即可。
K. Team Up
题目大意:有 \(n\) 种技能和 \(m\) 种角色,每种角色拥有若干个技能。任意两种角色拥有技能的集合互不相同,且要么互不相交,要么其中一个是另一个的子集。现在有 \(p\) 个玩家,每个玩家选择了一种角色,他们现在想要组队,每个队伍必须拥有所有的技能,问最多组多少支队,并输出方案。
题解:首先把技能树建出来,对包含每种技能的角色按集合大小排序即可。组队时在树上贪心。输出方案时启发式合并。
Dirt Replay
A: -1 swap 路径写错
D: -1 位置 i 不作为答案时转移错误
F: -4 写错了一堆,共产主义复用了一个数组
J: -1 D 坚持不用 W 的板子,写错了
K: -1 写错了
