Contest Info

date: 2018.11.08 19:49-24:49

practice link

Solutions

A. Nutella’s Life

题目大意： 求解这样一个 dp

\[ \text{dp}[i] = \max_{j<i,a_j\leq a_i} (\text{dp}[j] - \frac{(i-j)(i-j-1)}{2})+a_i \]

题解： 离散化 \(a\) 之后，树状数组套上双端队列然后斜率 dp。一个 \(\log\)。

B. Oleg and Data Science

签到题。

C. Christmas Garland

题目大意：

有\(n\le2\times10^5\)盏灯排成一行，第\(i\)盏灯的颜色为\(a_i\)，初始情况所有灯都是灭的.

\(q\le2\times10^5\)次操作，每次选择一种颜色，将这种颜色的所有灯的开关状态取反，之后询问有多少段极大的连续亮灯。

题解：

答案等价于求和每个位置它自己亮着且前一个位置没有亮着。

添加头尾两个额外的位置（颜色与其它位置不同且灯一直不亮），给相邻的两个颜色建无向边。

则等价于问图中多少条边的两端状态不同，然后答案除以二。

这样就是每次改变一个点，分度数大小是否超过\(O(\sqrt{n})\)处理一下即可。

时间复杂度\(O(n\sqrt{n})\)，空间复杂度\(O(n)\).

D. Anna and Lucky Tickets

题目大意：求所有长度为 \(n\)，满足奇数位置和等于偶数位置和的回文数的个数，允许有前导 \(0\)。

题解：若 \(n\) 是偶数，那么有对称的两个位置恰好一个在奇数位，一个在偶数位。因此所有的回文数都满足条件，即 \(10^{\frac{n}{2}}\) 个。

若 \(n\) 是奇数，我们可以得到一个形式为 \(a_{1}+\cdots+a_{s}-b_{1}-\cdots-b_{t}=c\) 的不定方程。左边的每个变量的取值范围都是 \([0,9]\)。我们把所有减号变成加号，再把两边加上 \(9t\) 后，不定方程变为 \(a_{1}+\cdots+a_{s+t}=c+9t\)，其中左边每个变量的取值范围是 \([0,9]\)。容斥即可。

F. Secret Permutation

题目大意： 交互题。有一个排列 \(p_0,\dots,p_{n-1}\)。 \(n\leq 5000\)。每次问 \((a,b,c)\)，回答 \(p^{-1}(p_a\cdot p_b+p_c)\)。最多问 \(12512\) 次。

题解：在 \(p^{-1}\) 里面构造出 \(0\)，那么就可以找到 \(0\) 的位置。容易发现 \(p_0(p_0+1)\cdots (p_{n-1}+1)\) 就是 \(0\)，那么我们问 \((x,i,x)(1\leq i\leq n)\)，其中 \(x\) 是上次的结果（初值为 \(0\)）。找到 \(0\) 之后，我们在剩下的位置中随机挑选两个位置 \(a,b\)，然后问 \((a,b,\text{pos}_0)\)，如果答案是 \(a\)，那么 \(b\) 还有可能是 \(1\)，把 \(b\) 放回去；答案是 \(b\) 同理。一直到最后只剩下一个数字，那么它就是 \(1\) 的位置。

我们接着问 \((\text{pos}_1,\text{pos}_{i-1},\text{pos}_1)\)，可以得到 \(\text{pos}_i\)。找到 \(0\) 和最后找到所有数字大概用了 \(10000\) 次，中间找 \(1\) 感受一下是 \(\frac{n}{2}\) 的。随机种子用 W 和 Z 的生日都过了。还要特殊判断一下 \(n=1\)。

H. Mikhail’s Problem

题目大意：

给出一个小写字母串\(s\)，\(1\le|s|\le10^5\).

给出\(1\le q\le10^5\)次询问，每次给出一个区间\([l_i,r_i]\)，问\(S[l_i\cdots r_i]\)中有多少本质不同的回文串。

题解：

考虑离线解决这个问题，如果我们能维护\(s\)的前缀\(i\)中每种回文串最后出现的开始位置集合\(left\)，那么询问\([l,i]\)的答案就是前缀\(i\)中本质不同的回文串减去\(left\)集合中小于\(l\)的元素个数。

很显然，\(left\)集合中不会有两个相同的位置，假如回文串\(u\)和\(v\)的\(left\)位置相同且\(|u|>|v|\)，那么由对称性，\(left + |u| - |v|\)也是\(v\)出现的开始位置，与\(left\)是\(v\)最后出现的开始位置矛盾。

假如我们已经得到了前缀\(i-1\)的\(left\)集合，对于前缀\(i\)，分增加的位置和减少的位置分别讨论。

那么对于前缀\(i\)，设\(u\)是前缀\(i\)最长的回文后缀，那么\(u\)的所有回文后缀\(v\)的\(left\)都会变为\(i-|v|+1\).

对于所有的这些\(i-|v|+1\)的位置，它们不属于前缀\(i-1\)的\(left\)集合，当且仅当\(link[v]=slink[v]\)成立。

设\(u=link[v]\)，如果\(u=\emptyset\)，显然，\(|v|=1\)，位置\(i\)不可能属于前缀\(i-1\)的\(left\)集合。

否则，由对称性，\(s[i-|v|+1\cdots i - |v| + |u|]=u​\)，如果\(i-|v|+1​\)不属于前缀\(i-1​\)的\(left​\)集合，一定存在一个位置\(i-|v|+1<j<i​\)使得\(j​\)也是\(u​\)出现的开始位置之一，否则上述结论成立。

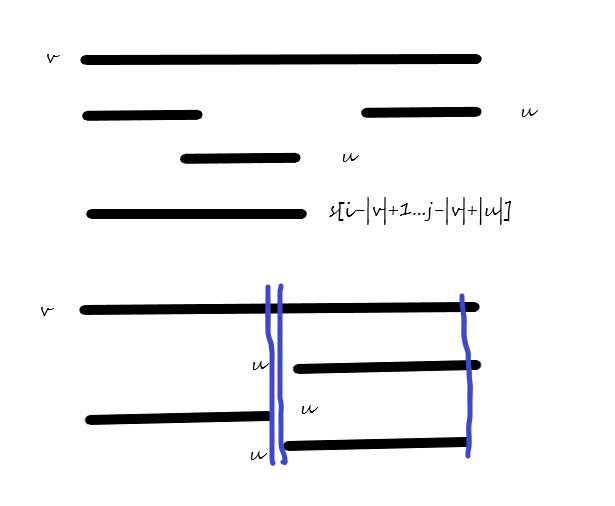
如果\(j\le i-|v|+|u|+1\)，那么\(2|u|\ge |s[i-|v|+1\cdots j+|u|-1]|\)，\(s[i-|v|+1\cdots j+|u|-1]\)有一个可以覆盖它的回文border，一定也是回文串，这与\(u=link[v]\)（\(u\)是\(v\)最长的回文border）矛盾。

因此\(j> i-|v|+|u|+1\)，\(|v|-1>2|u|\)，因此\(diff[u]\le|u|<|u|-|v|=diff[v]\)，\(link[v]=slink[v]\)成立。

所以\(left\)集合增加的位置，只有\(O(\log{n})\)个。

从增加的位置的讨论中，还可以得到一个结论，消失的\(left\)位置，一定是\(slink\)链上的\(v\)之前的\(left\)位置被\(i-|v|+1\)替换了，所以\(left\)集合删除的位置，也只有\(O(\log{n})\)个。

定义\(st[u]\)为\(u\)在\(link[u]\)链上最近的一个\(v\)满足\(link[v] = slink[v]\)，这样，将一个\(series\)的信息都用一个栈保存在\(st[u]\)处。

每个节点处的栈维护一个\((left,maxl)\)的二元组，并保证\(left\)严格单调增，\(maxl\)严格单调减，每个二元组表示\(series\)中\(|v|\le maxl\)的回文串\(v\)的最后出现位置不小于\(left+maxl-|v|\).

更新的时候\(i-|v|+1\)一定不会小于栈中的\(left\)，如果等号成立，\(|u|\)一定大于栈顶的\(maxl\)，因此直接更新栈顶元素即可。

如果更新之后栈中元素不少于\(2\)个，回文串\(v\)上一次的\(left\)位置一定是次栈顶元素的\(left+maxl-|v|\)处，把这个位置从\(left\)集合中删去即可。

之后，如果次栈顶元素的\(maxl\)等于\(|v|\)，则次栈顶元素就失效了，从栈中删去即可。

用树状数组维护\(left\)集合，则总的时间复杂度为\(O(n\log^2{n})\)，空间复杂度为\(O(n\log{n})\).

I. Rat-O-Matic

题目大意：

在二维平面上有\(n\le2\times10^5\)个相框.

第\(i\)个相框由两个中心都为\((x_i,y_i)\)的正方形组成，小正方形的边长为\(2r_i\)，大正方形的边长为\(4r_i\)，两个正方形之间的部分是相框，写着一个字母\(c_i\in\{r,a,t\}\).

任意两个相框都不相交也不会相切，只有包含和相离两种关系。

database中有\(m\)个字符串，只由\(rat\)三种字母组成，且总长度不超过\(2\times10^5\).

每个相框一开始都是出现的，接下来\(q\le2\times10^5\)次操作：

• \(-\quad x\)，让\(x\)号相框暂时消失
• \(+\quad x\)，让\(x\)号相框重新出现
• \(?\quad x\)，问从全部相框的外部，经过最少的相框到达\(x\)号相框内部，路径上的字母连起来的字符串\(s\)在database中多少个字符串中作为子串出现了

题解：

如果相框\(A\)包含\(B\)，则\(B\)的半径最多是\(A\)的一半。

扫描线求出包含关系树，则树高不超过\(\log{R}\).

将\(m\)个字符串，每个后缀的前\(\log{R}\)个前缀插入Trie中，询问时暴力走出\(s\)去Trie中询问即可。

时间复杂度\(O(n\log{n}+(m+q)\log{R})\).

J. Readability

题目大意：给你一个序列 \(a\)，要求你将它重排使得 \(a\) 奇偶相间。设重排后的序列为 \(\{a_{p_{i}}\}\)，则重排的代价为 \(\sum_{i=1}^{n}|p_{i}-i|\)。求代价最小的前提下字典序最小的 \(\{a_{p_{i}}\}\)。

题解：显然奇偶分别计算。那么问题就转化为了：有两个单调增的数列 \(a_{i}\) 和 \(b_{i}\)，且每个 \(a_{i}\) 有一个权 \(w_{i}\)。现在你要给出一个排列 \(p\)，使得 \(\sum_{i=1}^{n}|a_{p_{i}}-b_{i}|\) 最小，在此前提下，使得 \(\{w_{p_{i}}\}\) 字典序最小。

设有 \(i\neq j\) 满足 \(\max\{a_{p_{i}},b_{i}\}<\min\{a_{p_{j}}, b_{j}\}\)，那么容易证明 \(a_{p_{j}}\) 连接 \(b_{i}\)，\(a_{p_{i}}\) 连接 \(b_{j}\) 的代价一定比最优代价差。如图：

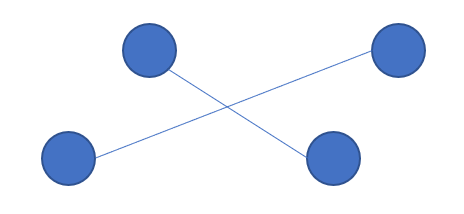
因此，我们可以将连续的 \(a_{i}<b_{i}\)，\(a_{i}=b_{i}\)，\(a_{i}>b_{i}\) 分别处理，因为不同的块之间连接必然会违反上面的规则。

对于 \(a_{i}=b_{i}\) 的块，显然 \(p_{i}=i\) 是代价最小的充要条件。此时不需要考虑字典序的问题。

对于 \(a_{i}<b_{i}\) 的块，容易证明 \(a_{p_{i}}\le b_{i}\) 对所有 \(i\) 成立是代价最小的充要条件。我们只需要用一个堆维护当前的 \(b_{i}\) 可匹配的 \(a_{i}\)，贪心地使字典序最大即可。

对于 \(a_{i}>b_{i}\) 的块，类似地有 \(a_{p_{i}}\ge b_{i}\) 对所有 \(i\) 成立是代价最小的充要条件。此时我们可以用一棵线段树维护每个 \(b_{i}\) 可匹配的 \(a_{i}\) 的数量，注意到这个数量是单调递减的，因此有解的充要条件是从右到左的每个 \(b_{i}\) 依次至少有 \(1,2,\cdots\) 个对应的 \(a_{i}\)。对每个 \(b_{i}\) 贪心地选取字典序最大可与它匹配且删去后不会导致无解的 \(a_{i}\) 即可。

时间复杂度 \(\mathcal{O}(n\log n)\)。

K. Robotobor

题目大意：

在一个\(n\times m\)的网格图中，\(n,m\le50\)，有一些格子是障碍，有一个唯一的起点\(S\)和一个唯一的终点\(T\).

定义一个路径为回文的，当且仅当这个路径总步数不超过\(100\)且它表示为\(L,R,U,D\)（向左一步，向右一步，向上一步，向下一步）的序列是回文的。

最小化从\(S\)走到\(T\)经过的路径数，输出方案。

题解：

首先求出出任意起点任意终点是否存在合法的回文路径，从路径\((u,u)\)和\((u,v)\)（\(u\)和\(v\)相邻）开始bfs，每次枚举一个方向向两端扩展即可。

然后再从s开始bfs一次就可以求出任意终点的答案。

输出方案只需记录两次bfs时的前驱即可。

时空复杂度\(O(n^2m^2)\).