Contest Info

practice link

Solutions

A. Parity

签到题。

B. Tape

签到题。

C. Meaningless Operations

签到题。

D. Jongmah

题目大意：给你一副麻将牌（当然每种可以不止 \(4\) 张），让你组出最多的顺子或刻子。

题解：可以认为同样的顺子最多出现两组，因为多于三组时可以组成三个刻子。然后就可以 \(dp\) 了。

E. Magic Stones

签到题。

F. Nearest Leaf

题目大意：给你一棵树，且树的结点编号与 dfs 序一致，边有边权，根不是叶子。有若干次询问，每次问一个点到编号属于 \([l,r]\) 的叶子的最短距离。

题解：离线做。假设当前在 \(1\) 号结点，求出它到每个叶子的距离，并用线段树维护。然后边 dfs 边回答当前点的询问，假设从 \(u\) 转移到孩子 \(v\)，那么 \(v\) 的子树中所有叶子的距离减去 \(w_{u,v}\)，其它的叶子加上 \(w_{u,v}\)。

G. Tree-Tac-Toe

题目大意：给你一棵树，开始有一些结点是白的，一些是透明的。现在两个人轮流玩游戏，先手白色，后手黑色，每人选择一个结点涂成自己的颜色。当某人有三个自己颜色的结点边成一条链时就获胜。问谁胜。

题解：后手是不可能赢的。不妨设开始没有白点，假设后手胜，就说明先手填任意一个白点时后手都能获胜。把颜色反过来，就说明先手在有一个黑点时仍能获胜，如果没有黑点就更能获胜。矛盾。也就是说我们只用判断先手是否能赢。

假如树中有一个白色结点 \(A\)，那么可以转成如下结构，其中 \(ABCD\) 都是无色的：

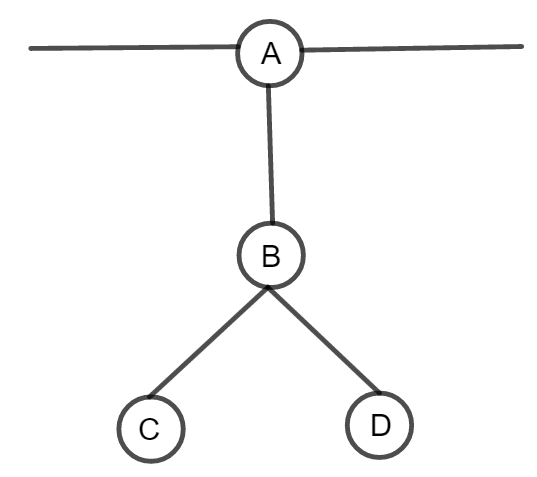
在这里，先手填一个 \(A\)，后手如果不填 \(B\) 就会输，所以他不一定会填 \(B\)。而 \(CD\) 两个人都赢不了，所以没人会去碰它们。这样就相当于先手白白有了一个结点。

图中黑色数字代表先手的操作，蓝色数字代表后手的操作。

假如有一个点度数大于等于 \(4\)，那么先手胜：

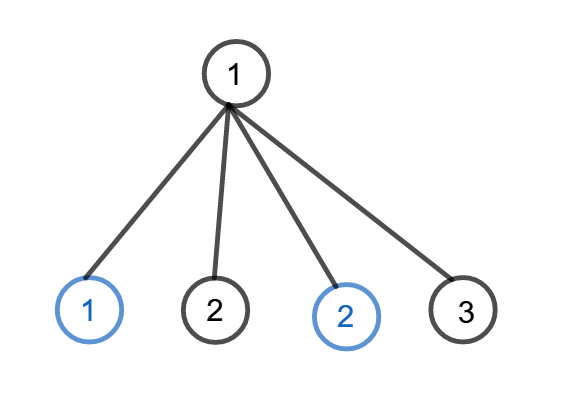
假如有一个点度数等于 \(3\)，且它的至少两棵子树 sz 至少为 \(2\)，那么先手胜：

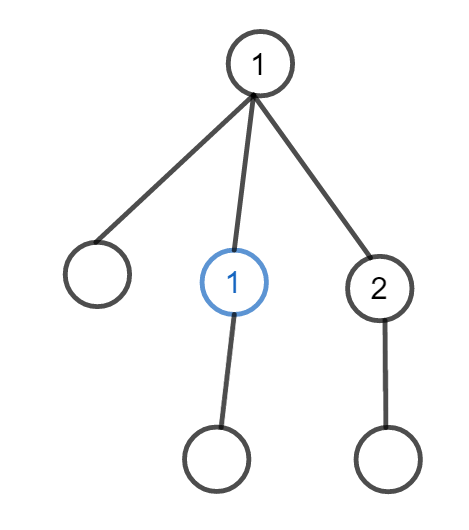
假如至少有三个度数等于 \(3\) 的点，那么就是上一种情况。

假如有一个或两个点度数等于 \(3\)，且不是上一种情况。那么这些度数为三的点一定在“两端”，我们可以把它们反过来变成白点。注意有两个点度数为 \(3\)，且为 \(6\) 和 \(7\) 个点时要特殊讨论，它们分别是平的和胜的。

现在的情况变成了一条链，两端可能是白点。假如两端都是白点，且链长为奇数，那么先手胜：

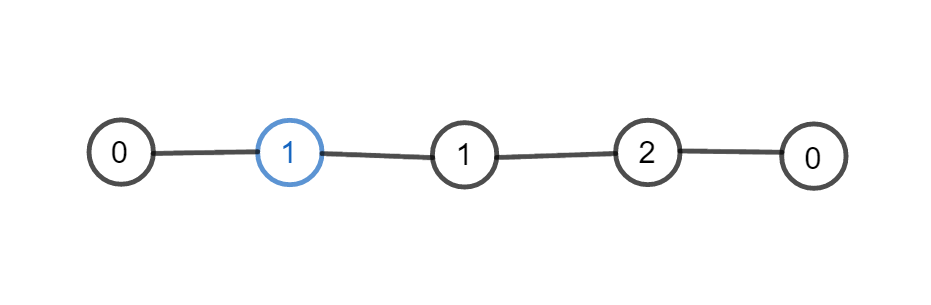
否则一定是平局，可以用归纳法证明。情况较多就不细讲了。

H. Modest Substrings

题目大意：给出 \(l\le r\le10^{800}\)，以及一个 \(n\le2000\)，求出长度为 \(n\) 的数字串中，含有 \([l,r]\) 中的数作为子串（子串中不得有前导 \(0\)）数量最多的数字串。若有多个，给出字典序最小的。

题解：我们按照数位 \(dp\) 的方法将 \([l,r]\) 中的数字分解成若干个互不相交的段。具体地说，以 \(l\) 和 \(r\) 长度相等时为例，可分解成 \(r_{1}r_{2}\cdots r_{i}[0-(r_{i+1}-1)][0-9]\{|r|-i-1\}\)，\(l_{1}l_{2}\cdots l_{i}[(l_{i+1}+1)-9][0-9]\{|l|-i-1\}\) 等形式（并没有列完，请自行体会）。

容易发现，把这些节点（不包括最后的通配符）建成 AC 自动机只有 \(\mathcal{O}(|l|+|r|)\Sigma)\) 个节点。设 \(dp[i][j]\) 表示当前处理了前 \(i\) 位，位于 AC 自动机的 \(j\) 节点，所有不同的子串的最大数量（只需要前面部分在前 \(i\) 位，而通配符部分是否在前 \(i\) 位无所谓，若有多个长度的通配符满足要求，要重复计算）。转移时，我们假设转移到 \(j'\) 节点，我们需要加上 \(j'\) 节点处不同长度且 \(\le n-i-1\) 的通配符种数，另外还要加上 \(\text{fail}[j'],\text{fail}[\text{fail}[j']],\cdots\)，一直到根。这些都可以在建 AC 自动机时预处理。

对于字典序最小的问题，我采取了这样的办法。\(dp\) 时记录当前最优解的字符串，但是每当字符串快要超出整型（比如 long long）时，就对其离散化一下，由于所有 \(dp[i][j]\) 的长度都为 \(i\)，这样离散化是不会改变相对大小的。好像之前没见过这种技巧？

时间复杂度 \(\mathcal{O}((|l|+|r|)n\Sigma^{2})\)。