Contest Info

practice link

Solutions

A. Array Without Local Maximums

签到题。

B. Multihedgehog

签到题。

C. Knights

题目大意：给你一个无限大的棋盘，让你在上面摆 \(n\) 个国际象棋中的骑士（攻击类似于中国象棋的马，但是没有“蹩马腿”），之后对于每个空位置，如果它受到 \(4\) 个骑士的攻击，在上面也摆一个骑士，一直到无法摆放为止。要求你构造一种方案，使得最后骑士数 \(\ge\lfloor\frac{n^{2}}{10}\rfloor\)。

题解：像这样摆放。

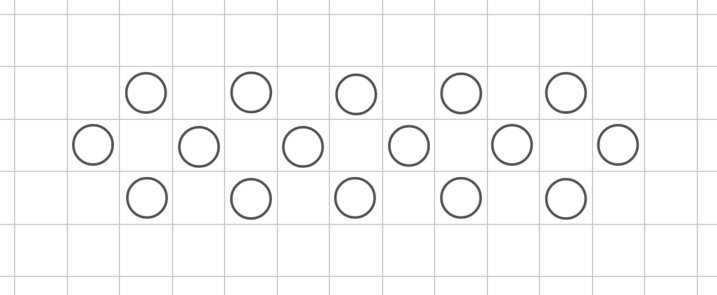
可以看出，每行中间的缝隙基本会被填满，然后向上、向下分别延伸出两个三角形，骑士的数量为 \(\mathcal{O}(\frac{n^{2}}{9})\)。

D. Computer Game

题目大意：有 \(n\le10^{5}\) 种游戏，每种游戏在升级前和升级后的奖励分别是 \(a_{i}\) 和 \(b_{i}(a_{i}<b_{i})\)，获胜的概率为 \(p_{i}\)。开始时所有的游戏都还没有升级。现在有 \(t\le10^{10}\) 秒的时间，每秒你可以选择一种游戏挑战，如果获胜，你会得到奖励，以及一次升级游戏的机会；如果失败，什么都得不到。问最大的期望收益。

题解：注意到，如果我们获得了一次升级机会，那么我们只要把 \(b_{i}p_{i}\) 最大的那个游戏升级，之后一直玩它就可以了。

设 \(dp_{t}\) 表示时间为 \(t\) 秒，且当前未升级的最大收益，记 \(P=\max_{1\le i\le n}b_{i}p_{i}\)，则有：

\[ \begin{aligned} dp_{t}&=\max_{1\le i\le n}(p_{i}(a_{i}+P(t-1))+(1-p_{i})dp_{t-1})\\ &=Pt+\max_{1\le i\le n}((1-p_{i})dp_{t-1}+p_{i}a_{i}-Pp_{i}) \end{aligned} \]

注意到这是一个斜率优化的形式，我们可以把下凸壳求出来。另外容易证明 \(dp\) 是单调增的，因此我们可以在凸壳的每一段上倍增。

时间复杂度 \(\mathcal{O}(n\log n+n\log t)\)。

E. Random Forest Rank

题目大意：给你一棵树，每条边有 \(\frac{1}{2}\) 的概率消失，求该森林的邻接矩阵的秩的期望。

题解：由于邻接矩阵是一个对称矩阵，因此秩等于最大非零主子式的阶数。考虑行列选取 \(S\) 的主子式，该矩阵表示了 \(S\) 的导出子图，仍是一个森林。

我们从行列式的定义出发，对于和式的某一项，\((-1)^{\pi(p)}\prod_{i=1}^{|S|}a_{i,p_{i}}\)。我们将排列 \(p\) 分解成若干个环，注意到森林只有长为 \(2\) 的环（一条边），因此该乘积不为 \(0\)，当且仅当排列是森林的一个完备匹配。而我们又知道森林若有完备匹配，那么就是唯一的，因此行列式非 \(0\)，当且仅当该森林有完备匹配。从而原森林的秩等于最大匹配（的点数）。

考虑一个森林如何求得最大匹配：设 \(dp[u][0/1]\) 表示点 \(u\) 未匹配/已匹配时的最大匹配。那么有：

\[ \begin{cases} dp[u][0]=\sum_{u\to v}\max(dp[v][0],dp[v][1])\\ dp[u][1]=1+\max_{u\to v}(dp[v][0]+\sum_{u\to w,w\neq v}\max(dp[w][0],dp[w][1])) \end{cases} \]

观察转移方程可知，如果存在某个儿子 \(v\) 满足 \(dp[v][0]=dp[v][1]\)，那么 \(dp[u][1]=dp[u][0]+1\)；否则 \(dp[u][1]=dp[u][0]\)。那么在原问题中，我们就可以用 \(dp_{1}[u][0/1]\) 表示，\(dp[u][1]=dp[u][0]+(0/1)\) 的方案分别有多少种。转移很简单。最后统计答案时容易发现，当且仅当 \(dp[u][1]=dp[u][0]+1\) 时我们会增加一条匹配边，因此统计一下每个 \(dp_{1}[u][1]\) 的贡献即可。